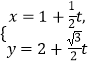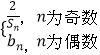��Ŀ����
����Ŀ����֪ԲM��![]() ��
��![]() ������
������
(1)��![]() ��ֵ��
��ֵ��
(2)��ԲM��![]() ���Ͻصõ��ҳ���
���Ͻصõ��ҳ���
(3)����![]() ��ֱ��
��ֱ��![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ��ֱ��
��ֱ��![]() ��ԲM���У�
��ԲM���У�![]() Ϊ�е㣬���ı���
Ϊ�е㣬���ı���![]() �������Сֵ��
�������Сֵ��
���𰸡�(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
�����������������(1)�Ƚ�Բ��һ�㷽�̻��ɱ����̣�����ֱ�ߺ�Բ���н��������(2) ��![]() ���õ�����
���õ�����![]() ��һԪ���η��̽��������(3)���ı��ε��������Сֵ����ת��Ϊ�㵽ֱ�ߵĵľ���������.
��һԪ���η��̽��������(3)���ı��ε��������Сֵ����ת��Ϊ�㵽ֱ�ߵĵľ���������.
���������(1) ![]() ������ԲM��
������ԲM��![]() ��
��![]() ��������
��������
��![]() ��������
��������![]()
(2) ��![]() ����
����![]() ������
������![]()
����![]()
(3) ![]()
����![]() ����Сֵ���ڵ�
����Сֵ���ڵ�![]() ��ֱ��
��ֱ��![]() �ľ��룬��
�ľ��룬��
��![]() ����
����![]()
���ı���![]() �������СֵΪ
�������СֵΪ![]() ��
��
�����͡������
��������
20
����Ŀ����ƽ��ֱ������ϵ![]() �У�Բ
�У�Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() ����Բ
����Բ![]() ��
��![]() �ύ��
�ύ��![]() ��
�� ![]() ���㣬��ֱ��
���㣬��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
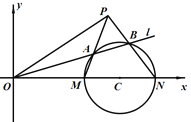
��1����ֱ��![]() ��Բ
��Բ![]() ����ʱ����ֱ��
����ʱ����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����ֱ֪��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ��
�� ![]() ���㣮
���㣮
��������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
��
�Ƿ���ڳ���![]() ��ʹ��
��ʹ��![]() ������������ڣ����
������������ڣ����![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��������
����3��������
�������������������1��������![]() ��Բ��
��Բ��![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ����ֱ��
����ֱ��![]() ��Բ
��Բ![]() ���е�
���е�![]() ���ɴ������ֱ��
���ɴ������ֱ��![]() �ķ��̣���2����i��������ã�
�ķ��̣���2����i��������ã� ![]() ��
�� ![]() ���ɴ������ʵ��
���ɴ������ʵ��![]() ��ȡֵ��Χ��(ii)
��ȡֵ��Χ��(ii) ![]() ��Բ
��Բ![]()
![]() �������ã�
�������ã� ![]() ����Τ�ﶨ�����
����Τ�ﶨ�����![]() �����꣬�Ӷ��õ�
�����꣬�Ӷ��õ�
![]() ���ɴ���֤�����ڳ���
���ɴ���֤�����ڳ���![]() ��ʹ��
��ʹ��![]() �������
�������
�����������1���⣺�����⣬ ![]() ��
��
��Բ��![]() ��ֱ��
��ֱ��![]() �ľ���
�ľ���![]() ��
��
��ֱ��![]() ��Բ
��Բ![]() ���У���
������![]() ��
��
��![]() ����ֱ��
����ֱ��![]() ��
��
��2���⣺������ã� ![]() ����
����![]() ��
��
�ɣ�1����֪�� ![]() ����
���� ��
��
��![]() ��
��
��3��֤���� ![]() ����Բ
����Բ![]()
![]() �������ã�
�������ã� ![]() ��
��
��![]() ��
�� ![]() ����
���� ��
��
ͬ���ɵã�  �� ��
�� ��![]() ��
��
�� ����
����![]() ��
��
��![]() ����
����![]() �� ��
�� ��![]() ��
��
�� ����
���� �� ��
�� �� ����
����![]() ��
��
�� ����
����![]() ��
��
����ڳ���![]() ��ʹ��
��ʹ��![]() �������
�������
���������硿������Ҫ�������ϵ������ֱ�߷��̡�ֱ����Բ��λ�ù�ϵ�Լ����������еĴ��������⣬��������.������������⣬�ȼ�����ڣ���֤���������Ľ��ۣ���������ȷ����ڣ������۲���ȷ���ڣ�ע�⣺�ٵ������ͽ��۲�ΨһʱҪ�������ۣ��ڵ��������۶�Ҫ�Ƶ������ڵ�����ʱ���ȼ�����������Ƴ��������۵������ͽ��۶���֪�������淽�������ʱ��ȡ�����;��.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�