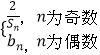题目内容
【题目】已知函数![]() ,且
,且![]() 时,总有
时,总有![]() 成立.
成立.
![]() 求a的值;
求a的值;
![]() 判断并证明函数
判断并证明函数![]() 的单调性;
的单调性;
![]() 求
求![]() 在
在![]() 上的值域.
上的值域.
【答案】(1)![]() (2)函数
(2)函数![]() 为R上的减函数(3)
为R上的减函数(3) ![]()
【解析】试题分析: ![]() 根据条件建立方程关系
根据条件建立方程关系![]() 即可求a的值;
即可求a的值;
![]() 根据函数单调性的定义判断并证明函数
根据函数单调性的定义判断并证明函数![]() 的单调性;
的单调性;
![]() 结合函数奇偶性和单调性的定义即可求
结合函数奇偶性和单调性的定义即可求![]() 在
在![]() 上的值域.
上的值域.
试题解析:
![]() ,
, ![]() ,即
,即![]() ,
,
![]() ,
,
![]() .
.
![]() 函数
函数![]() 为R上的减函数,
为R上的减函数,
![]() 的定义域为R,
的定义域为R,
![]() 任取
任取![]() ,且
,且![]() ,
,
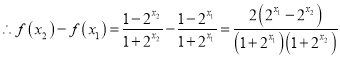 .
.
![]() .
.
![]() 即
即![]()
![]() 函数
函数![]() 为R上的减函数.
为R上的减函数.
![]() 由
由![]() 知,函数
知,函数![]() 在
在![]() 上的为减函数,
上的为减函数,
![]() ,
,
即![]() ,
,
即函数的值域为![]() .
.
点晴:证明函数单调性的一般步骤:(1)取值:在定义域上任取![]() ,并且
,并且![]() (或
(或![]() );(2)作差:
);(2)作差: ![]() ,并将此式变形(要注意变形到能判断整个式子符号为止);(3)定号:判断
,并将此式变形(要注意变形到能判断整个式子符号为止);(3)定号:判断![]() 的正负(要注意说理的充分性),必要时要讨论;(4)下结论:根据定义得出其单调性.
的正负(要注意说理的充分性),必要时要讨论;(4)下结论:根据定义得出其单调性.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下面是某日水深的数据:
t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y/m | 10 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 10 |
经长期观察,y=f(t)的曲线可以近似地看成函数![]() 的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
(1)求y与t满足的函数关系式;
(2)某船吃水深度(船底离水面的距离)为6.5m,如果该船希望在同—天内安全进出港,请问该船在什么时间段能够安全进港?它同一天内最多能在港内停留多少小时?(忽略进 出港所需的时间).