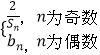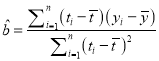Question

【题目】已知函数 ， ．
（I）求 的单调区间；
（II）若对任意的 ，都有 ，求实数 的取值范围．

Answer 1

【答案】解：（I） ， 当 时， 恒成立，则 在 上单调递增；当 时，令 ，则 ．则 在区间 上单调递增，在区间 上单调递减．

（II） ， 等价于 .令 ，则 ．

令 ，则 ．

因为当 ， 恒成立，

所以 在 上单调递减．

又 ，可得 和 在 上的情况如下：

	+	0	-
	单调递增		单调递减

所以 在 上的最大值为 ．

因此 ， 等价于 ．

故 ， 时，实数 的取值范围是 ．

【解析】(1)根据题意求出导函数利用导函数的性质即可得到原函数的单调性。(2)根据题意 x ∈ ( 0 , + ∞ ) ， f ( x ) ≤ 2 a 2 等价,构造函数 g ( x )，对其求导利用导函数的性质能求出 x ∈ ( 0 , + ∞ ) ， f ( x ) ≤ 2 a 2 时，即可求出a的取值范围。
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案，需要熟知一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．