Question

【题目】已知函数f（x）=x2﹣alnx+x（a∈R）
（Ⅰ）当a=1时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
（Ⅱ）讨论函数y=f（x）的单调性．

Answer 1

【答案】解：（Ⅰ）当a=1时，f（x）=x2﹣lnx+x，f（1）=2，此时点A（1，2）， ， ∴切线的斜率k=f′（1）=2，
∴切线方程为：y﹣2=2（x﹣1），
即y=2x
（Ⅱ）由题意知：f（x）的定义域为（0，+∞），
令g（x）=2x2+x﹣a（x＞0）
（i）当△=1+8a≤0，即 时，g（x）≥0，
∴x∈（0，+∞），f′（x）≥0，
∴f（x）为（0，+∞）的单调递增函数；
（ii）当△=1+8a＞0，即 时，此时g（x）=0有两个根： ，
①若 时，f′（x）≥0，x∈（0，+∞）
②若 a＞0时，当 ；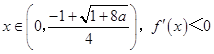
当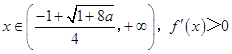
综上可知：（i）当 时时，f（x）为（0，+∞）的单调递增函数；
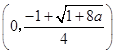（ii）当 时，f（x）的减区间是 ，增区间是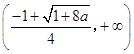
【解析】（Ⅰ）求导函数，可得切线的斜率，求出切点坐标，利用点斜式可得切线方程；（Ⅱ）确定函数的定义域，求导函数，分类讨论，利用导数的正负，可讨论函数y=f（x）的单调性．
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．