题目内容
16.若方程xe-x-a+1=0有两个不相等的实数根,则a的取值范围是(1,1+$\frac{1}{e}$).分析 方程xe-x-a+1=0有两个不相等的实数根可化为ex=$\frac{x}{a-1}$有两个不相等的实数根,再化为函数y=ex与y=$\frac{x}{a-1}$的交点个数问题,从而作函数的图象,结合导数求解.
解答 解:∵方程xe-x-a+1=0有两个不相等的实数根,
∴方程xe-x=a-1有两个不相等的实数根,
而当a-1=0时,方程xe-x=a-1只有一个根0,故不成立;
故a-1≠0;
故ex=$\frac{x}{a-1}$有两个不相等的实数根,
作函数y=ex与y=$\frac{x}{a-1}$的图象如下,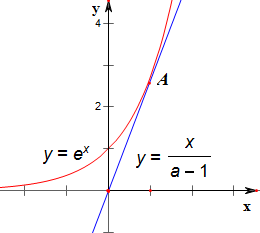
设切点为A(x,ex);
则ex=$\frac{{e}^{x}}{x}$;
故x=1;
即切线的斜率k=e;
$\frac{1}{a-1}$>e;
解得,1<a<1+$\frac{1}{e}$;
故答案为:(1,1+$\frac{1}{e}$).
点评 本题考查了方程的根与函数的图象的交点的关系应用,同时考查了切线的斜率与导数的几何意义的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知x>1,y>1且x+y=20.则lgx+lgy的最大值是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
11.若函数f(x)=x3-mx2-x+5在区间(0,1)内单调递减,则实数m的取值范围是( )
| A. | m≥1 | B. | m=1 | C. | m≤1 | D. | 0<m<1 |
1.复数z=3-i的虚部是( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
5.若$\frac{sinα}{1+cosα}$=$\frac{1}{2}$,则sinα的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{8}{5}$ | C. | 1 | D. | $\frac{29}{15}$ |
6.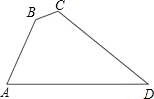 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 4+$\sqrt{6}$ | D. | 2+2$\sqrt{6}$ |