题目内容
6．函数$f（x）=3sin（-2x+\frac{π}{3}）$的单调增区间是[kπ+$\frac{5π}{12}$ kπ+$\frac{11π}{12}$]，k∈Z．分析 由于f（x）=-3sin（2x-$\frac{π}{3}$），利用正弦函数的单调性求得函数f（x）的增区间．
解答 解：对于函数$f（x）=3sin（-2x+\frac{π}{3}）$=-3sin（2x-$\frac{π}{3}$），令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$，k∈Z，
求得kπ+$\frac{5π}{12}$≤x≤kπ+$\frac{11π}{12}$，故函数f（x）的增区间为 $[\frac{5π}{12}+kπ，\frac{11π}{12}+kπ]，k∈Z$，
故答案为：[kπ+$\frac{5π}{12}$ kπ+$\frac{11π}{12}$]，k∈Z．
点评 本题主要考查正弦函数的单调性，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
16．已知$sinθ=\frac{4}{5}$，$cosθ=-\frac{3}{5}$，则2θ是（ ）
| A． | 第一象限角 | B． | 第二象限角 | C． | 第三象限角 | D． | 第四象限角 |
17．f（x）=-$\frac{1}{2}$x2+bln（x+2）在（-1，+∞）上单调递减，则b的取值范围是（ ）
| A． | （-∞，-1） | B． | （-1，+∞） | C． | [-1，+∞） | D． | （-∞，-1] |
1．把函数$y=sin（2x+\frac{π}{3}）$的图象向左平移φ（|φ|＜$\frac{π}{2}$）个单位后得到的图象关于y轴对称，则φ的最小正值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$ |
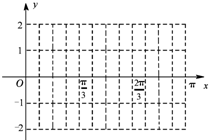设函数f（x）=2sin（2x+φ）（0＜φ＜π），y=f（x）图象的一个对称中心是$（\frac{π}{3}，0）$．