题目内容
6.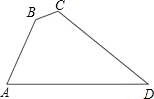 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 4+$\sqrt{6}$ | D. | 2+2$\sqrt{6}$ |
分析 过点A,D分别作AE,DF垂直于直线BC,垂足分别为E,F,求出EF,FD的值,然后过点A作AG⊥DF,垂足为G,AG=EF=4+$\sqrt{6}$,FG=GD=$\sqrt{6}$,在RT△?ADG中,根据勾股定理得AD的长.
解答 解:如图,过点A,D分别作AE,DF垂直于直线BC,垂足分别为E,F,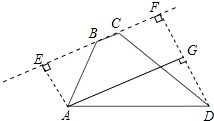
由已知可得BE=AE=$\sqrt{6}$,CF=2$\sqrt{2}$,DF=2$\sqrt{6}$,于是EF=4+$\sqrt{6}$
过点A作AG⊥DF,垂足为G,则AG=EF=4+$\sqrt{6}$,FG=GD=$\sqrt{6}$,在RT△?ADG中,根据勾股定理得
AD=$\sqrt{(4+\sqrt{6})^{2}+(\sqrt{6)^{2}}}$=$\sqrt{28+8\sqrt{6}}$=$\sqrt{24+2×2\sqrt{24}+4}$=$\sqrt{({\sqrt{24}+2)}^{2}}$=2+2$\sqrt{6}$
故选:D
点评 本题考查了三角函数在三角形中的应用,属于中档题.

练习册系列答案
相关题目