题目内容
4．已知不等式x2-3x+2≥0的解集为A，不等式$\frac{x-3}{x}$≤-1的解集为B，不等式x2-（a+1）x+a＜0的解集为C（1）求A∩B
（2）若A∪C=R，求a的取值范围．
分析 求出集合A、BC，然后求解
（1）A∩B
（2）通过A∪C=R，直接求a的取值范围．
解答 解：不等式x2-3x+2≥0的解集为A={x|x≤1或x≥2}，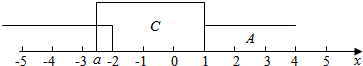
不等式$\frac{x-3}{x}$≤-1的解集为B={$x|0＜x≤\frac{3}{2}$}，
（1）A∩B={x|0＜x≤1}
（2）A={x|x≤1或x≥2}，
A∪C=R，不等式x2-（a+1）x+a＜0化为（x-1）（x-a）＜0，由数轴可知：a≥2．
点评 本题考查不等式的解法，集合的交、并、补的基本运算，基本知识的考查．
练习册系列答案
相关题目
