题目内容
8.用与球心距离为2的平面去截球,所得的截面面积为π,则球的体积为( )| A. | $\frac{20π}{3}$ | B. | $\frac{20\sqrt{5}π}{3}$ | C. | 20$\sqrt{5}$π | D. | $\frac{100π}{3}$ |
分析 求出小圆的半径,利用球心到该截面的距离为2,小圆的半径,通过勾股定理求出球的半径,即可求出球的体积.
解答 解:用一平面去截球所得截面的面积为π,所以小圆的半径为1.
已知球心到该截面的距离为2,所以球的半径为r=$\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$,
所以球的体积为:$\frac{4}{3}π(\sqrt{5})^{3}=\frac{20\sqrt{5}π}{3}$;
故选B.
点评 本题考查球的小圆的半径、球心到该截面的距离、球的半径之间的关系,考查计算能力,是基础题.

练习册系列答案
相关题目
19.某校高一年级有200人,其中100人参加数学第二课堂活动.在期末考试中,分别对参加数学第二课堂活动的同学与未参加数学第二课堂活动的同学的数学成绩进行调查.按照学生数学成绩优秀与非优秀人数统计后,构成如下不完整的2×2列联表:
已知p是(1+2x)5展开式中的第三项系数,q是(1+2x)5展开式中的第四项的二项式系数.
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
(Ⅰ)求p与q的值;
(Ⅱ)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩优秀与参加数学第二课堂活动有关”.
16.若圆C的圆心为(2,1),且经过原点O,则圆C的标准方程是( )
| A. | (x-2)2+(y-1)2=$\sqrt{5}$ | B. | (x-2)2+(y-1)2=5 | C. | (x+2)2+(y+1)2=$\sqrt{5}$ | D. | (x+2)2+(y+1)2=5 |
3.已知两个实数a、b(a≠b)满足aea=beb,命题p:lna+a=lnb+b;命题q:(a+1)(b+1)<0.则下面命题是真命题的是( )
| A. | p∨(¬q) | B. | p∧(¬q) | C. | p∨q | D. | p∧q |
13.执行如图所示的程序框图,若输入x的值为2+log23,则输出y的值为( )
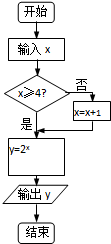

| A. | $\frac{8}{3}$ | B. | 8 | C. | 12 | D. | 24 |
20.已知f(x)=x3+ax2+bx+a2在x=1处的极值为10,则a+b=( )
| A. | 0或-7 | B. | -7 | C. | 0 | D. | 7 |
13.在等差数列{an}中,2an+1=an+an+2成立.类比上述性质,在等比数列{bn}中,有( )
| A. | 2bn+1=bn+bn+2 | B. | bn+12=bn•bn+2 | C. | 2bn+1=bn•bn+2 | D. | bn+12=bn+bn+2 |