��Ŀ����
19��ijУ��һ�꼶��200�ˣ�����100�˲μ���ѧ�ڶ����û������ĩ�����У��ֱ�Բμ���ѧ�ڶ����û��ͬѧ��δ�μ���ѧ�ڶ����û��ͬѧ����ѧ�ɼ����е��飮����ѧ����ѧ�ɼ����������������ͳ�ƺ������²�������2��2��������| ���� | ������ | �ܼ� | |
| �μ���ѧ�ڶ����û | p | ||
| δ�μ���ѧ�ڶ����û | q | 100 | |
| �ܼ� | 200 |
������p��q��ֵ��
��������������2��2�����������ж�����99%�Ŀɿ���Ҫ���ܷ���Ϊ���ɼ�������μ���ѧ�ڶ����û�йء���
���� �������ã�1+2x��5 ��չ��ʽͨ�ʽ���p��q��ֵ��
�����ɣ���p=40��q=10�����K2��ֵ���ٸ���P��K2��6.635��=0.010���ó����ۣ�
��� �⣺���ߣ�1+2x��5 ��չ��ʽͨ�ʽ��Tr+1=${C}_{5}^{r}$•��2x��r��
��չ��ʽ�ĵ������ǣ�T3=${C}_{5}^{2}$•4•x2=40x2��
��������ϵ����p=40��
�֡�չ��ʽ�ĵ�����Ķ���ʽϵ��Ϊ${C}_{5}^{3}$=10����q=10��
�����ɣ���p=40��q=10����
| ���� | ������ | �ܼ� | |
| �μ���ѧ�ڶ����û | 40 | 60 | 100 |
| δ�μ���ѧ�ڶ����û | 10 | 90 | 100 |
| �ܼ� | 50 | 150 | 200 |
������99%�Ŀɿ���Ҫ���ܹ��жϳɼ�������μ���ѧ�ڶ����û�йأ�
���� ������Ҫ�������ʽ������Ӧ�ã�����ʽչ��ʽ��ͨ�ʽ�������Եļ��飬�����е��⣮

��ϰ��ϵ�д�
 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�
�����Ŀ
10��ƫ����ָ����ⶨֵ��ⶨ��ƽ��ֵ֮��ڳɼ�ͳ���У����ǰ�ij��ͬѧ��ij�ƿ��Գɼ���ÿư�ƽ���ֵIJ��ij��ƫ���ij�ο��Գɼ�ͳ���У�ij��ʦΪ�˶�ѧ����ѧƫ��x����λ���֣�������ƫ��y����λ���֣�֮��Ĺ�ϵ���з����������ѡ��8λͬѧ���õ����ǵ����Ƴɼ�ƫ���������£�
������x��y֮�����������ع�ϵ����y����x�����Իع鷽�̣�
�������ôο��Ըð���ѧƽ����Ϊ120�֣�����ƽ����Ϊ91.5�֣����ɣ�1���Ľ���Ԥ����ѧ�ɼ�Ϊ128�ֵ�ͬѧ�������ɼ���
�ο����ݣ�
$\sum_{i=1}^{8}$xiyi=20��6.5+15��3.5+13��3.5+3��1.5+2��0.5+��-5������-0.5��+��-10������-2.5��+��-18������-3.5��=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+��-5��2+��-10��2+��-18��2=1256��
| ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ��ѧƫ��x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| ����ƫ��y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
�������ôο��Ըð���ѧƽ����Ϊ120�֣�����ƽ����Ϊ91.5�֣����ɣ�1���Ľ���Ԥ����ѧ�ɼ�Ϊ128�ֵ�ͬѧ�������ɼ���
�ο����ݣ�
$\sum_{i=1}^{8}$xiyi=20��6.5+15��3.5+13��3.5+3��1.5+2��0.5+��-5������-0.5��+��-10������-2.5��+��-18������-3.5��=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+��-5��2+��-10��2+��-18��2=1256��
7����֪һ���ε�Բ�ĽǵĻ�����Ϊ2���仡��Ҳ��2��������ε����Ϊ��������
| A�� | 1 | B�� | 2 | C�� | sin1 | D�� | 2sin1 |
14�����ʱ�µ������ȣ�ij��λ�ԡ�ϲ��������ְ���Ա��Ƿ��йء�������һ�ε��飬������ְ����60�ˣ�Ůְ����������ְ��������$\frac{1}{2}$��ϲ����������ְ����������ְ��������$\frac{1}{6}$��ϲ��������Ůְ��������Ůְ��������$\frac{2}{3}$��
��1����������������������2��2��������
��2���ܷ��ڷ�����ĸ��ʲ�����0.001��ǰ������Ϊϲ��������ְ���Ա��й�ϵ��
�ο����ݼ���ʽ��
K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$������n=a+b+c+d��
��1����������������������2��2��������
| ϲ������ | ��ϲ������ | �ܼ� | |
| ��ְ�� | |||
| Ůְ�� | |||
| �ܼ� |
�ο����ݼ���ʽ��
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
11��������ĸo��o��r��t������У����ŵ�root�ĸ���Ϊ��������
| A�� | $\frac{1}{24}$ | B�� | $\frac{1}{12}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{1}{2}$ |
8���������ľ���Ϊ2��ƽ��ȥ�������õĽ������Ϊ�У���������Ϊ��������
| A�� | $\frac{20��}{3}$ | B�� | $\frac{20\sqrt{5}��}{3}$ | C�� | 20$\sqrt{5}$�� | D�� | $\frac{100��}{3}$ |
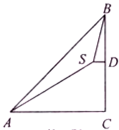 ��ͼ����ɽ��A�����ɽ��B�����ǡ�CAB=45�㣬����б��Ϊ30���б��AS��2000����S�㣬�ֲ��ɽ����DSB=75�㣬��ɽ��BCΪ2000�ף�
��ͼ����ɽ��A�����ɽ��B�����ǡ�CAB=45�㣬����б��Ϊ30���б��AS��2000����S�㣬�ֲ��ɽ����DSB=75�㣬��ɽ��BCΪ2000�ף�