题目内容
14.某地A、B两村在一直角坐标系下的位置分别为A(1,2),B(4,0),一条河所在直线的方程为l:x+2y-10=0,若在河上建一座水站P,使分别到A、B两镇的管道之和最省,问供水站P应建在什么地方?分析 根据两点间的距离公式以及点的对称性,建立方程组关系进行求解即可.
解答 解:过A作直线l的对称点A′,连A′B交l于P,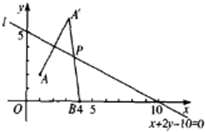
∵|AP′|+|P′B|=|A′P′|+|BP′|>|A′B|,
∴P点即为所求.
设A′(a,b),则$\left\{\begin{array}{l}{\frac{a+1}{2}+2•\frac{b+2}{2}-10=0}\\{\frac{b-2}{a-1}•(-\frac{1}{2})=-1}\end{array}\right.$,
即$\left\{\begin{array}{l}{a+2b=15}\\{b=2a}\end{array}\right.$,解得a=3,b=6,
即A′(3,6),
直线A′B的方程为$\frac{y-0}{6-0}=\frac{x-4}{3-4}$,即6x+y-24=0,
由$\left\{\begin{array}{l}{6x+y-24=0}\\{x+2y-10=0}\end{array}\right.$,解得x=$\frac{38}{11}$,y=$\frac{36}{11}$,
即P($\frac{38}{11}$,$\frac{36}{11}$),
故供水站P应建在P($\frac{38}{11}$,$\frac{36}{11}$),才能使管道最省.
点评 本题主要考查直线对称性的应用,以及直线交点坐标的求解,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
8.用与球心距离为2的平面去截球,所得的截面面积为π,则球的体积为( )
| A. | $\frac{20π}{3}$ | B. | $\frac{20\sqrt{5}π}{3}$ | C. | 20$\sqrt{5}$π | D. | $\frac{100π}{3}$ |
19.设a=sin33°,b=cos58°,c=tan34°,则( )
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |