题目内容
18.已知函数f(x)=x2+ax+1,a为实数.(1)解不等式f(x)>0,
(2)当x>0时,不等式f(x)≥0恒成立,求a的取值范围.
分析 (1)根据判别式分类讨论求出不等式的解集,
(2)分离参数,根据基本不等式即可求出a的取值范围.
解答 解:(1)△=a2-4,
①当△>0,即a>2或a<-2时,不等式的解集为(-∞,$\frac{-a-\sqrt{{a}^{2}-4}}{2}$)∪($\frac{-a+\sqrt{{a}^{2}-4}}{2}$,+∞),
②当△=0,即a=2或-2时,
当a=2时,不等式的解集为(-∞,-1)∪(-1,+∞);
当a=-2时,不等式的解集为(-∞,1)∪(1,+∞);
③当△<0,即当-2<a<2时,解集为R.
综上,①当a>2或a<-2时,不等式的解集为(-∞,$\frac{-a-\sqrt{{a}^{2}-4}}{2}$)∪($\frac{-a+\sqrt{{a}^{2}-4}}{2}$,+∞);
②当a=2时,不等式的解集为(-∞,-1)∪(-1,+∞);
③当a=-2时,不等式的解集为(-∞,1)∪(1,+∞);
④当-2<a<2时,解集为R.
(2)当x>0时,由x2+ax+1≥0得a≥-(x+$\frac{1}{x}$)=-2$\sqrt{x•\frac{1}{x}}$=-2,当且仅当x=1时取等号.
故a的取值范围为[-2,+∞)
点评 本题考查了一元二次不等式的解法和基本不等式的应用,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.若函数f(x)=$\left\{\begin{array}{l}{\sqrt{2-{x}^{2}},-\sqrt{2}≤x≤1}\\{\frac{1}{x},1<x≤e}\end{array}\right.$,则${∫}_{-\sqrt{2}}^{e}$f(x)dx等于( )
| A. | $\frac{3π+6}{4}$ | B. | $\frac{3π+4}{4}$ | C. | π+1 | D. | $\frac{3π+3}{2}$ |
10.偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,在某次考试成绩统计中,某老师为了对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
(Ⅰ)若x与y之间具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:
$\sum_{i=1}^{8}$xiyi=20×6.5+15×3.5+13×3.5+3×1.5+2×0.5+(-5)×(-0.5)+(-10)×(-2.5)+(-18)×(-3.5)=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+(-5)2+(-10)2+(-18)2=1256.
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(Ⅱ)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:
$\sum_{i=1}^{8}$xiyi=20×6.5+15×3.5+13×3.5+3×1.5+2×0.5+(-5)×(-0.5)+(-10)×(-2.5)+(-18)×(-3.5)=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+(-5)2+(-10)2+(-18)2=1256.
7.已知一扇形的圆心角的弧度数为2,其弧长也是2,则该扇形的面积为( )
| A. | 1 | B. | 2 | C. | sin1 | D. | 2sin1 |
8.用与球心距离为2的平面去截球,所得的截面面积为π,则球的体积为( )
| A. | $\frac{20π}{3}$ | B. | $\frac{20\sqrt{5}π}{3}$ | C. | 20$\sqrt{5}$π | D. | $\frac{100π}{3}$ |
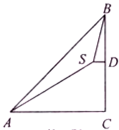 如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.
如图,在山底A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的斜坡AS走2000米至S点,又测得山顶∠DSB=75°,则山高BC为2000米.