题目内容
已知与曲线C: x2+y2-2x-2y+1=0相切的直线l与x轴、y轴的正半轴交于两点A、B，O为原点，|OA|＝a，|OB|=b(a>2,b>2)
（1）求证：曲线C与直线l相切的条件是(a-2)(b-2)="2" ;
（2）求ΔAOB面积的最小值。
（1）求证：曲线C与直线l相切的条件是(a-2)(b-2)="2" ;
（2）求ΔAOB面积的最小值。
(1)证明见解析(2)
(1)直线l的方程为
即bx+ay-ab=0
圆心O到直线l的距离d=
,
当d=1时，直线与圆相切,
即=1
整理得(a-2)(b-2)=2
所以曲线C与直线l相切的条件是(a-2)(b-2)=2.
(2)
当且仅当a=2+
时等号成立.
即bx+ay-ab=0
圆心O到直线l的距离d=
,当d=1时，直线与圆相切,
即
=1整理得(a-2)(b-2)=2
所以曲线C与直线l相切的条件是(a-2)(b-2)=2.
(2)
当且仅当a=2+
时等号成立.
练习册系列答案
浙江名校名师金卷系列答案
相关题目
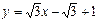绕点（1，1）顺时针旋转，使它与圆
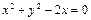相切，则直线转动的最小正角是 。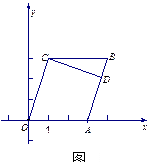
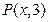向圆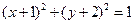
引切线，则切线长度的最小值等于（ ）．
，求圆心到直线
的距离的取值范围.(14分)
=0与直线y=－1相切,且其圆心在y轴的左侧,则m的值为__________.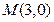
是圆
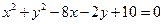内一点，过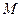
点最长的弦所在的直线的
