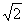题目内容
已知圆心在直线2x+y=0上，且过点A（2，－1），与直线x－y－1=0相切，求圆的方程。
圆的方程为:(x－1)2+(y+2)2=2或(x－9)2+(y+18)2=338
由圆心在直线2x+y=0上，设圆心坐标为(x0,－2x0)∵过点A（2，－1）且与直线x－y－1=0相切，∴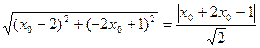
,解得x0=1或x0=9当x0=1时，半径r=
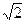，当x0=9时，半径r=
,
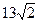∴所求圆的方程为:(x－1)2+(y+2)2=2或(x－9)2+(y+18)2=338
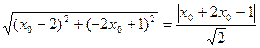,解得x0=1或x0=9当x0=1时，半径r=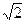，当x0=9时，半径r=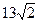,∴所求圆的方程为:(x－1)2+(y+2)2=2或(x－9)2+(y+18)2=338
练习册系列答案
相关题目
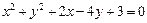
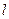与圆C相切，且直线
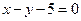距离的最大值与最小值
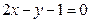被圆
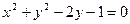所截得的弦长为 ．
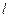的距离为2，Q是
(φ为参数,m>0)相切，则m为
