题目内容
已知函数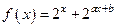 ,且f(1)=
,且f(1)=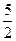 ,f(2)=
,f(2)=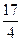 .(1)求
.(1)求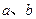 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在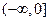 上的单调性,并证明。
上的单调性,并证明。
解:(1)由已知得: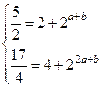 ,解得
,解得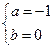 .
.
(2)由上知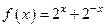 .任取
.任取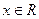 ,则
,则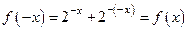 ,所以
,所以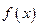 为偶函数.
为偶函数.
解析

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
题目内容
已知函数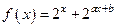 ,且f(1)=
,且f(1)=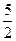 ,f(2)=
,f(2)=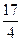 .(1)求
.(1)求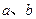 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在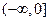 上的单调性,并证明。
上的单调性,并证明。
解:(1)由已知得: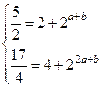 ,解得
,解得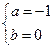 .
.
(2)由上知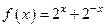 .任取
.任取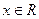 ,则
,则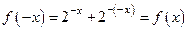 ,所以
,所以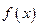 为偶函数.
为偶函数.
解析

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案