题目内容
已知函数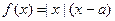 ,
,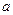 为实数.
为实数.
(1)当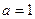 时,判断函数
时,判断函数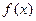 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)当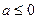 时,指出函数
时,指出函数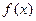 的单调区间(不要过程);
的单调区间(不要过程);
(3)是否存在实数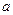
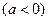 ,使得
,使得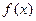 在闭区间
在闭区间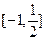 上的最大值为2.若存在,求出
上的最大值为2.若存在,求出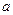 的值;若不存在,请说明理由
的值;若不存在,请说明理由
(1)


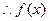 既不是奇函数,又不是偶函数. ……………………………………4分
既不是奇函数,又不是偶函数. ……………………………………4分
(2)(画图)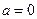 时,
时, ,单调增区间为
,单调增区间为
 时,
时,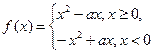 ,
,
单调增区间为 ,单调减
,单调减 区间为
区间为 ………………………………8分
………………………………8分
(3)



由(2)知,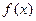 在
在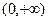 上递增
上递增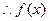 必在区间
必在区间 上取最大值2 ……………………………………10分
上取最大值2 ……………………………………10分
当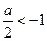 ,即
,即 时,
时,
则 ,
, ,成立 ……………………………………12分
,成立 ……………………………………12分
当 ,即
,即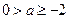 时,
时,
则 ,则
,则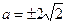 (舍)
(舍)
综上,
解析

练习册系列答案
相关题目
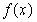 ,对任意的
,对任意的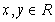 ,有
,有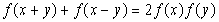 ,且
,且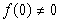 .
.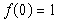 ; (2)求证:
; (2)求证: 的定义域为
的定义域为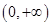 ,对于任意正实数
,对于任意正实数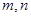 恒有
恒有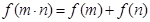 ,且当
,且当 时,
时,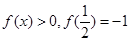
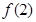 的值;
的值; 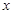 的不等式
的不等式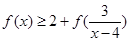 .
.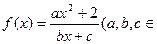 Z)是奇函数,又
Z)是奇函数,又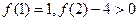 ,
,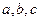 的值。
的值。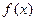 满足关系式
满足关系式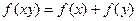 且
且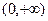 上是增函数
上是增函数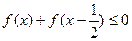
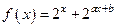 ,且f(1)=
,且f(1)=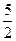 ,f(2)=
,f(2)=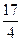 .(1)求
.(1)求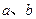 ;(2)判断
;(2)判断 f(x)的奇偶性;(3)试判断函数在
f(x)的奇偶性;(3)试判断函数在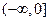 上的单调性,并证明。
上的单调性,并证明。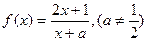 ,
, ,证明
,证明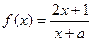 在区间
在区间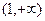 上是增函数;
上是增函数;
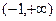 上是单调函数,试求实数
上是单调函数,试求实数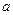 的取值范围。
的取值范围。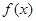 的最小值为1,且
的最小值为1,且 .
.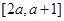 上不单调,求实数
上不单调,求实数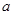 的取值范围;
的取值范围;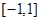 上,
上,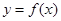 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数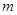 的
的 取值范围。
取值范围。