题目内容
已知函数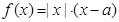
．
（I）判断
的奇偶性；
（Ⅱ）设函数在区间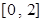
上的最小值为
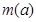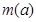，求的表达式；
（Ⅲ）若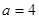
，证明：方程
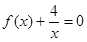有两个不同的正数解．
（I）既不是奇函数也不是偶函数
（Ⅱ）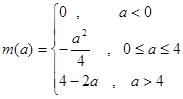
（Ⅲ）见解析
解析
练习册系列答案
手拉手全优练考卷系列答案
相关题目
手拉手全优练考卷系列答案题目内容
已知函数．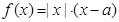
（I）判断的奇偶性；
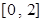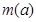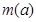（Ⅱ）设函数在区间上的最小值为，求的表达式；
（Ⅲ）若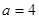，证明：方程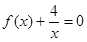有两个不同的正数解．
（I）既不是奇函数也不是偶函数
（Ⅱ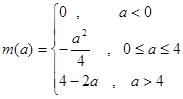）（Ⅲ）见解析
解析
手拉手全优练考卷系列答案
且
，
的奇偶性；
时,求使
成立的实数
的取值范围. 
的导函数
，
，
、
为实数。
，
）处切线的斜率为12，求
，求函数
．（1）求
的单调区间；（2）当
时，求函数
在区间
上的最小值．
的定义域为
，对于任意正实数
恒有
，且当
时，
的值； 
的不等式
．
Z）是奇函数，又
,
的值。
，且f（1）＝
，f（2）＝
．（1）求
；（2）判断
f（x）的奇偶性；（3）试判断函数在
上的单调性，并证明。
，
，
，
为常
对所有实数成立的充要条件（用
表示）；
为两实数，
且
,若
在区间
上的单调增区间的长度和为
（闭区间
的长度定义为
）．
|x|在x∈[－1,1]的图象上有两点A、B，
AB∥