题目内容
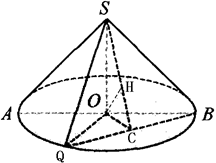
(本题满分14分).如图,圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上的一点,如果QB的中点为C,OH⊥SC,垂足为H。
求证:BQ⊥平面SOC,
求证:OH⊥平面SBQ;设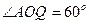 ,
,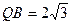 ,求此圆锥的体积。
,求此圆锥的体积。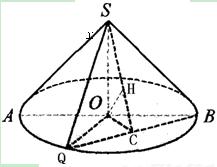
求证:BQ⊥平面SOC,
求证:OH⊥平面SBQ;设
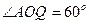 ,
,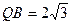 ,求此圆锥的体积。
,求此圆锥的体积。
略
(1)证明:轴截面SAB为等腰直角三角形,SO⊥平面ABQ, 1分
BQ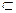 平面ABQ ∴SO⊥BQ 2分
平面ABQ ∴SO⊥BQ 2分
在圆O中,弦BC的中点为C
所以 OC⊥BQ 3分
又∵OC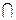 SO="O " 4分
SO="O " 4分
∴BQ⊥平面SOC 5分
(2)由(1)知道BQ⊥平面SOC,
∵OH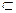 平面SOC
平面SOC
∴BQ⊥OH 7分
由已知OH⊥SC,且BQ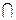 SC="C " 9分
SC="C " 9分
∴OH⊥平面SBQ; 10分
(3)C为BQ中点,又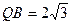 ∴
∴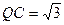 , 11分
, 11分
∵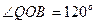 ,∴
,∴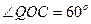
在直角三角形QCO中,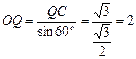 12分
12分
由于轴截面SAB为等腰直角三角形,那么OS=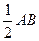 ="2 " 13分
="2 " 13分
∴圆锥的体积V= 14分
14分

BQ
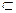 平面ABQ ∴SO⊥BQ 2分
平面ABQ ∴SO⊥BQ 2分在圆O中,弦BC的中点为C
所以 OC⊥BQ 3分
又∵OC
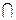 SO="O " 4分
SO="O " 4分∴BQ⊥平面SOC 5分
(2)由(1)知道BQ⊥平面SOC,
∵OH
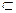 平面SOC
平面SOC ∴BQ⊥OH 7分
由已知OH⊥SC,且BQ
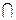 SC="C " 9分
SC="C " 9分∴OH⊥平面SBQ; 10分
(3)C为BQ中点,又
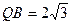 ∴
∴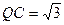 , 11分
, 11分∵
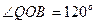 ,∴
,∴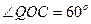
在直角三角形QCO中,
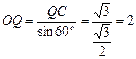 12分
12分由于轴截面SAB为等腰直角三角形,那么OS=
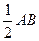 ="2 " 13分
="2 " 13分∴圆锥的体积V=
 14分
14分
练习册系列答案
相关题目

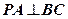 ;
; 中,
中,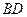 为AC边上的高,
为AC边上的高,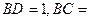
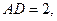 沿BD将
沿BD将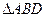 翻折,使得
翻折,使得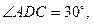 得到几何体
得到几何体
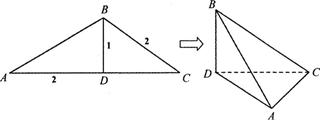
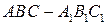 中,
中, 分别是
分别是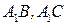 的中点,点
的中点,点
 在
在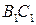 上,
上,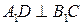
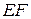 ∥平面
∥平面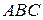
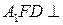 平面
平面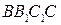
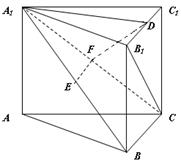
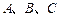 在球心为
在球心为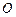 的球面上,
的球面上,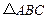 的内角
的内角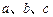 ,且
,且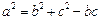 ,
,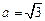 ,球心
,球心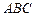 的距离为
的距离为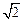 ,则该球的表面积为 .
,则该球的表面积为 .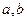 是夹角为
是夹角为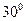 的异面直线,则满足条件“
的异面直线,则满足条件“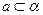 ,
,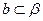 ,且
,且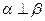 ”的平面
”的平面 ,
,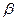 ( )
( )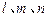 及平面
及平面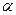 ,下列命题中的假命题是 ( )
,下列命题中的假命题是 ( )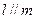 ,
,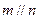 ,则
,则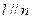
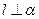 ,
,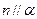 ,则
,则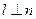
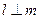 ,
,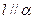 ,
, 在底半径为
在底半径为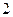 ,高为
,高为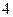 的圆锥中内接一个的圆柱,圆柱的最大侧面积为_______
的圆锥中内接一个的圆柱,圆柱的最大侧面积为_______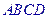 各边
各边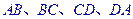 上分别取
上分别取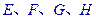 四点,如果与
四点,如果与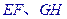 能相交于点
能相交于点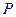 ,那么( )
,那么( ) 上
上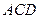 外
外 外
外