题目内容
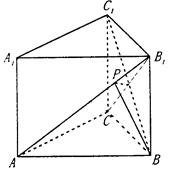
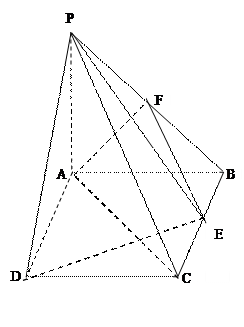
(本小题满分12分)如图在三棱锥P-ABC中,PA=3,AC=AB=4,PB=PC=BC=5,D、E分别是BC、AC的中点,F为PC上的一点,且PF:FC=3:1。

(Ⅰ)求证: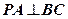 ;
;
(Ⅱ)试在PC上确定一点G,使平面ABG//平面DEF;
(Ⅲ)在满足(Ⅱ)的情况下,求直线GB与平面ABC所成角的正弦值。

(Ⅰ)求证:
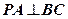 ;
;(Ⅱ)试在PC上确定一点G,使平面ABG//平面DEF;
(Ⅲ)在满足(Ⅱ)的情况下,求直线GB与平面ABC所成角的正弦值。
(Ⅰ)
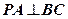 ,证明略。
,证明略。(Ⅱ)取
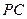 的中点
的中点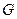 ,则点
,则点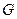 可使平面
可使平面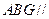 平面
平面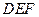 ,证明略。
,证明略。(Ⅲ)
解:
(Ⅰ)在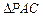 中,∵PA=3,AC=4,PC=5,
中,∵PA=3,AC=4,PC=5,
∴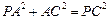 ,∴
,∴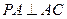 ,同理可得
,同理可得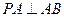
∵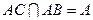 ,∴
,∴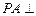 平面ABC
平面ABC
∵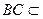 平面ABC,∴
平面ABC,∴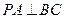 。
。
(Ⅱ)如图所示取PC的中点G,则点G可使平面ABG//平面DEF。
连结AG、BG,∵PF:FC=3:1,∴F为GC的中点
又D、E分别是BC、AC的中点,
∴AG//EF,同时易知BG//FD,又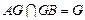 ,
,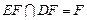
∴平面ABG//平面DEF,即PC的中点G可使平面ABG//平面DEF。
(Ⅲ)由(Ⅱ))知G为PC的中点,连结GE,则有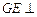 平面ABC,连接EB,
平面ABC,连接EB,
则EB是GB在平面ABC内的射影,
所以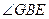 是
是 与平面ABC所成的角,而
与平面ABC所成的角,而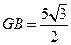 ,
,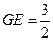 ,
,
所以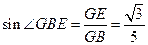 ,所以直线
,所以直线 与平面ABC所成角的正弦值是
与平面ABC所成角的正弦值是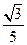 。
。
(Ⅰ)在
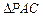 中,∵PA=3,AC=4,PC=5,
中,∵PA=3,AC=4,PC=5,∴
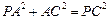 ,∴
,∴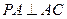 ,同理可得
,同理可得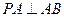
∵
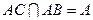 ,∴
,∴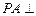 平面ABC
平面ABC∵
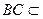 平面ABC,∴
平面ABC,∴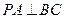 。
。(Ⅱ)如图所示取PC的中点G,则点G可使平面ABG//平面DEF。
连结AG、BG,∵PF:FC=3:1,∴F为GC的中点
又D、E分别是BC、AC的中点,
∴AG//EF,同时易知BG//FD,又
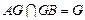 ,
,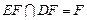
∴平面ABG//平面DEF,即PC的中点G可使平面ABG//平面DEF。
(Ⅲ)由(Ⅱ))知G为PC的中点,连结GE,则有
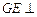 平面ABC,连接EB,
平面ABC,连接EB,则EB是GB在平面ABC内的射影,
所以
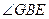 是
是 与平面ABC所成的角,而
与平面ABC所成的角,而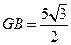 ,
,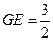 ,
,所以
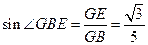 ,所以直线
,所以直线 与平面ABC所成角的正弦值是
与平面ABC所成角的正弦值是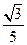 。
。
练习册系列答案
相关题目
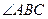 的度数为
的度数为 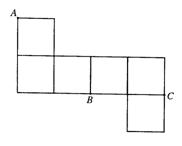
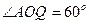 ,
,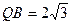 ,求此圆锥的体积。
,求此圆锥的体积。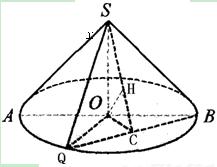
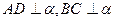 ,AD=4,
,AD=4, ,
,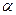 内的轨迹是 ( )
内的轨迹是 ( )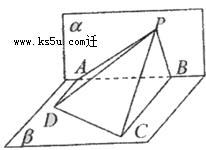
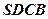 中,
中,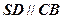 ,
,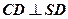 ,
,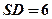 ,
,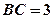 ,
,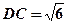 ,
,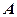 是
是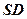 的中点,
的中点,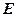 是线段
是线段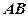 的中点,沿
的中点,沿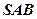 折起到平面
折起到平面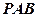 的位置,使
的位置,使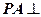 平面
平面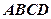 ,则下列命题正确的个数是 。
,则下列命题正确的个数是 。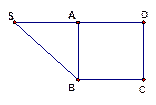
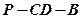 成角
成角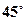 ;
;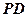 的中点
的中点 ,则
,则 平面
平面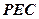 ;
;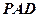 所成的锐二面角的大小为
所成的锐二面角的大小为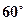 ;
;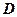 到平面
到平面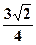
 是异面直线,
是异面直线, ,
,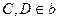 ,
,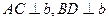 ,且
,且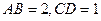 ,则
,则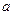 与
与 所成的角是( )
所成的角是( )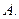


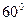


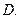
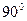
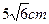 的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm .
的正四面体内有一点P,它到三个面的距离分别是1cm,2cm,3cm,则它到第四个面的距离为_______________cm .