题目内容
设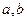 是夹角为
是夹角为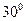 的异面直线,则满足条件“
的异面直线,则满足条件“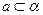 ,
,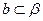 ,且
,且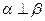 ”的平面
”的平面 ,
,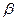 ( )
( )
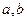 是夹角为
是夹角为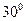 的异面直线,则满足条件“
的异面直线,则满足条件“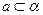 ,
,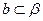 ,且
,且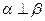 ”的平面
”的平面 ,
,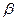 ( )
( )| A.不存在 | B.有且只有一对 |
| C.有且只有两对 | D.有无数对 |
D
略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
题目内容
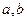 是夹角为
是夹角为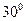 的异面直线,则满足条件“
的异面直线,则满足条件“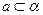 ,
,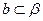 ,且
,且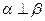 ”的平面
”的平面 ,
,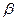 ( )
( )| A.不存在 | B.有且只有一对 |
| C.有且只有两对 | D.有无数对 |

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案