��Ŀ����
����Ŀ��ij�н�������Ϊ�˽�ȫ�и���ѧ�������߷���������ӱ���ȫ�����ѧ���������ȡ��100�˵��������ݽ���ͳ�Ʒ����������ݴ����õ�������ͼ1��ʾ��Ƶ�·ֲ�ֱ��ͼ����������100��ѧ���У����߲�����1.69��ѧ��ֻ��16���������߾�Ҷͼ����ͼ2��ʾ��������������Ƶ�ʹ��Ƹ��и�һѧ�������߸��ʣ�
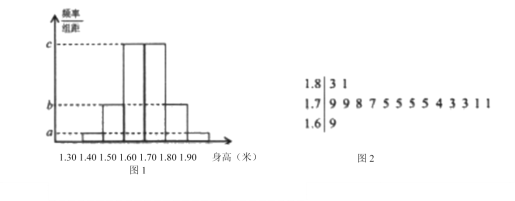
��1������и���ѧ�����߸���1.70�ĸ��ʣ�����ͼ1��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2�����Ӹ��и���ѧ�������ѡȡ3��ѧ������![]() Ϊ������
Ϊ������![]() ��ѧ����������
��ѧ����������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��3��������![]() ����
����![]() ��
��![]() ����Ʊ���
����Ʊ���![]() �����������̬�ֲ�
�����������̬�ֲ�![]() �ĸ��ʷֲ���������и���ѧ�������������������̬�ֲ�
�ĸ��ʷֲ���������и���ѧ�������������������̬�ֲ�![]() �ĸ��ʷֲ�������Ϊ���и���ѧ�������߷��������������ģ����жϸ��и���ѧ�������߷��������Ƿ���������˵�����ɣ�
�ĸ��ʷֲ�������Ϊ���и���ѧ�������߷��������������ģ����жϸ��и���ѧ�������߷��������Ƿ���������˵�����ɣ�
���𰸡���1������Ϊ0.15��![]() ��
��![]() ��
��![]() ����2����������3������
����2����������3������
����������������1�������ø��ʹ�ʽ������ѧ�������߸���1.70�ĸ��ʣ�����![]() ��
��![]() ��
��![]() ���Ӷ��õ�a,b,c��ֵ.(2)�����������
���Ӷ��õ�a,b,c��ֵ.(2)�����������![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]() �����ݶ���ֲ���
�����ݶ���ֲ���![]() �ķֲ��к���ѧ����.(3)����
�ķֲ��к���ѧ����.(3)����![]() ��
��![]() ���ٸ�����֪�жϸ��и���ѧ�������߷��������Ƿ�����.
���ٸ�����֪�жϸ��и���ѧ�������߷��������Ƿ�����.
��⣺��1����ͼ2��֪��100������ѧ�������߸���1.70����15������������Ƶ�ʹ�������ĸ��ʣ��ɵ�����ѧ�������߸���1.70�ĸ���Ϊ0.15��
��![]() Ϊѧ�������ߣ����ͼ1�ɵã�
Ϊѧ�������ߣ����ͼ1�ɵã�
![]() ��
��
![]() ��
��
![]() ��
��
���������Ϊ0.1������![]() ��
��![]() ��
��![]() ��
��
��2����������Ƶ�ʹ�������ĸ��ʣ�
��֪������ѧ�������ѡȡ1����������![]() �ĸ���Ϊ
�ĸ���Ϊ
![]() ��
��
��Ϊ������ѧ�������ѡȡ3�����൱�������ظ��������飬
�����������![]() ���Ӷ���ֲ�
���Ӷ���ֲ�![]() ��
��
�ֲ���Ϊ��![]() ��
��
| 0 | 1 | 2 | 3 |
| 0.027 | 0.189 | 0.441 | 0.343 |
![]() ����
����![]() ��
��
��3����![]() ��ȡ
��ȡ![]() ��
��![]() ��
��
�ɣ�2����֪��![]() ��
��
�ֽ�ϣ�1�����ɵã�![]() ��
��
![]() ��
��
��������ѧ�������������������̬�ֲ�![]() �ĸ��ʷֲ���Ӧ����Ϊ���и�һѧ�������߷��������������ģ�
�ĸ��ʷֲ���Ӧ����Ϊ���и�һѧ�������߷��������������ģ�

����Ŀ�����ij��мƻ����¶���һ�����̣�ÿ���������ͬ�������ɱ�ÿƿ4Ԫ���ۼ�ÿƿ6Ԫ��δ�۳������̽��۴�������ÿƿ2Ԫ�ļ۸���ȫ��������![]() �����������۾��飬ÿ���������뵱���������
�����������۾��飬ÿ���������뵱���������![]() ��λ��
��λ��![]() �й�
�й�![]() ���������²�����25��������Ϊ500ƿ������������λ������
���������²�����25��������Ϊ500ƿ������������λ������![]() ��������Ϊ300ƿ�����������µ���20��������Ϊ200ƿ
��������Ϊ300ƿ�����������µ���20��������Ϊ200ƿ![]() Ϊ��ȷ�����·ݵĶ����ƻ���ͳ����ǰ�������·�ÿ�������������ݣ��õ������Ƶ���ֲ�����
Ϊ��ȷ�����·ݵĶ����ƻ���ͳ����ǰ�������·�ÿ�������������ݣ��õ������Ƶ���ֲ�����
������� |
|
|
|
|
|
|
���� | 2 | 16 | 36 | 25 | 7 | 4 |
��1�������·���������һ���������������300ƿ��Ƶ�ʣ�
��2�������·���һ���������̵Ľ�����Ϊ450ƿʱ������һ�������������̵�ƽ������λ��Ԫ��
����Ŀ��ij���п�����ͨ��һ���ֻ�APP������������ij��1000���ܲ�������ƽ��ÿ�ܵ��ܲ�������ơ��������������õ����µ�Ƶ���ֲ���
��������km/�ܣ� |
|
|
|
|
|
|
|
|
|
���� | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
��1���ڴ���ϲ�ȫ����1000���ܲ���������������Ƶ�ʷֲ�ֱ��ͼ:

ע:������Ǧ�ʻ���ȷ�������ú�ɫˮ�����
��2����������ͼ�����ݼ����������ƽ����Ϊ![]() ��������������λ��������һλС����������ƽ��������λ���������������Ƹ����ܲ��������������ķֲ��ص�
��������������λ��������һλС����������ƽ��������λ���������������Ƹ����ܲ��������������ķֲ��ص�
��3�������ܲ������ߵ������������ܲ������߷ֳ��������࣬��ͬ�������߹����װ���ļ۸�һ�������±�:
������ | С��20���� | 20���ﵽ40���� | ��С��40���� |
��� | �������� | �������� | ��Ӣ���� |
װ���۸�λ��Ԫ�� | 2500 | 4000 | 4500 |
�����������ݣ����Ƹ���ÿλ�ܲ������߹���װ����ƽ����Ҫ���Ѷ���Ԫ?



