题目内容
(本题满分13分)已知圆 :
:
(1) 若平面上有两点 (1 , 0),
(1 , 0), (-1 , 0),点P是圆
(-1 , 0),点P是圆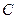 上的动点,求使
上的动点,求使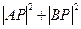 取得最小值时点
取得最小值时点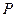 的坐标.
的坐标.
(2)若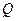 是
是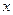 轴上的动点,
轴上的动点,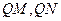 分别切圆
分别切圆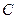 于
于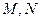 两点
两点
① 若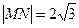 ,求直线
,求直线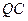 的方程;
的方程;
② 求证:直线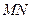 恒过一定点.
恒过一定点.
 :
:
(1) 若平面上有两点
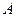 (1 , 0),
(1 , 0),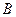 (-1 , 0),点P是圆
(-1 , 0),点P是圆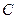 上的动点,求使
上的动点,求使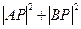 取得最小值时点
取得最小值时点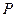 的坐标.
的坐标. (2)若
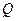 是
是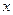 轴上的动点,
轴上的动点,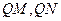 分别切圆
分别切圆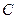 于
于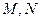 两点
两点① 若
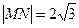 ,求直线
,求直线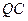 的方程;
的方程;② 求证:直线
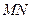 恒过一定点.
恒过一定点.解:(1)设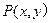 , 则由两点之间的距离公式知
, 则由两点之间的距离公式知
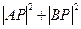 =
=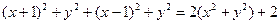 =2
=2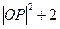
要使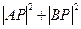 取得最小值只要使
取得最小值只要使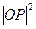 最小即可
最小即可
又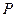 为圆上的点,所以
为圆上的点,所以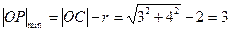 (
(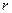 为半径)
为半径)
∴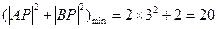 此时直线
此时直线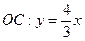 ,由题意:
,由题意:
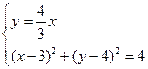 解得
解得 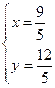 或
或 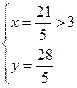 (舍去)
(舍去)
∴点 的坐标为
的坐标为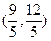 ………………5分
………………5分
(2) ①设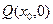 因为圆
因为圆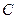 的半径
的半径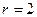 , 而
, 而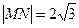 则
则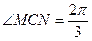 ,
,
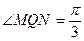 而
而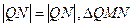 为等边三角形。
为等边三角形。
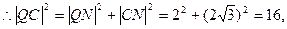
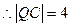
所求直线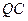 的方程:
的方程: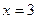 ………………9分
………………9分
②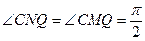 则
则 是以
是以 为直径的圆上。设
为直径的圆上。设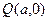 则
则
以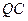 为直径的圆
为直径的圆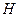 的方程:
的方程: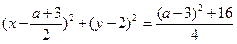 即
即
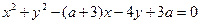 与圆
与圆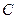 :
: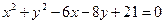 联立,消去
联立,消去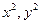 得
得
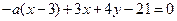 ,故无论取
,故无论取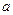 何值时,直线
何值时,直线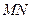 恒过一定点
恒过一定点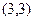 .
. 

 ………………13分
………………13分
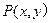 , 则由两点之间的距离公式知
, 则由两点之间的距离公式知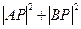 =
=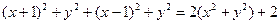 =2
=2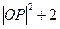
要使
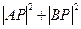 取得最小值只要使
取得最小值只要使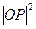 最小即可
最小即可又
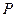 为圆上的点,所以
为圆上的点,所以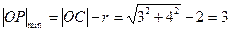 (
(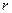 为半径)
为半径) ∴
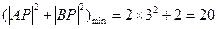 此时直线
此时直线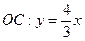 ,由题意:
,由题意: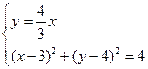 解得
解得 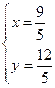 或
或 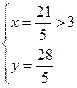 (舍去)
(舍去)∴点
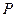 的坐标为
的坐标为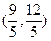 ………………5分
………………5分(2) ①设
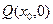 因为圆
因为圆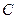 的半径
的半径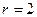 , 而
, 而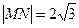 则
则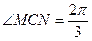 ,
,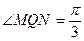 而
而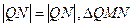 为等边三角形。
为等边三角形。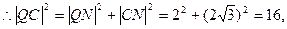
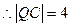
所求直线
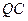 的方程:
的方程: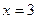 ………………9分
………………9分②
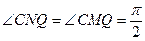 则
则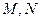 是以
是以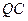 为直径的圆上。设
为直径的圆上。设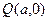 则
则以
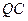 为直径的圆
为直径的圆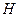 的方程:
的方程: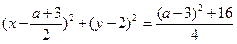 即
即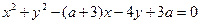 与圆
与圆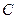 :
: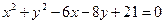 联立,消去
联立,消去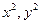 得
得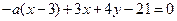 ,故无论取
,故无论取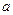 何值时,直线
何值时,直线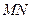 恒过一定点
恒过一定点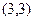 .
. 

 ………………13分
………………13分略

练习册系列答案
相关题目
 为直径端点作圆,所作圆与
为直径端点作圆,所作圆与 轴有交点
轴有交点 ,则交点
,则交点



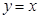 上一点
上一点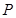 引圆
引圆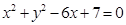 的切线,则切线长的最小值为
的切线,则切线长的最小值为



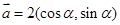 ,
,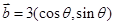 ,若
,若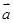 与
与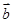 的夹角为
的夹角为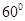 ,则直线
,则直线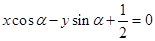 与圆
与圆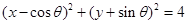 的位置关系是( )
的位置关系是( ) 和
和 的值而定
的值而定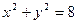 内有一点
内有一点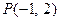 ,
,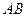 为过点
为过点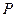 的直线。
的直线。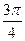 时,求弦
时,求弦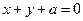 与圆
与圆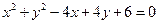 有交点,则实数
有交点,则实数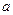 的取值范围是( )
的取值范围是( )