题目内容
(本题满分12分)已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P、Q两点.
(Ⅰ)求实数m的取值范围;
(Ⅱ)求以PQ为直径且过坐标原点的圆的方程.
(Ⅰ)求实数m的取值范围;
(Ⅱ)求以PQ为直径且过坐标原点的圆的方程.
解:(Ⅰ)
(法一)圆C: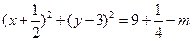 ,圆心
,圆心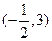 ,半径
,半径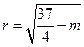
圆心到直线的距离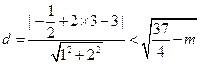 ,得
,得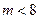 ;(4分)
;(4分)
(法二)由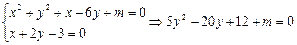 ,有
,有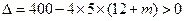 ,得m<8;(或者联立得
,得m<8;(或者联立得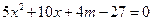 )(4分)
)(4分)
(Ⅱ)设P(x1,y1), Q(x2,y2),由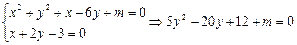
∴
由于以PQ为直径的圆过原点,∴OP⊥OQ, ∴x1x2+y1y2=0,
而x1x2=9-6(y1+y2)+4y1y2=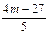 ,∴
,∴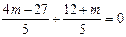 解得m=3.(8分)
解得m=3.(8分)
故P(1,1), Q(-3,3),圆的方程为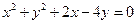 ,即
,即 .(12分)
.(12分)
(法二)设过PQ的圆的方程为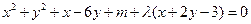
∴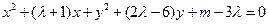 ,
,
即
∵圆过原点,∴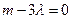 ,又以PQ为直径,则
,又以PQ为直径,则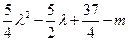 取最小值,此时
取最小值,此时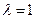 ,故m=3,圆的方程为
,故m=3,圆的方程为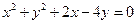 ,即
,即 .(12分)
.(12分)
(法一)圆C:
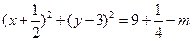 ,圆心
,圆心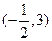 ,半径
,半径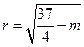
圆心到直线的距离
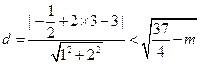 ,得
,得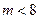 ;(4分)
;(4分)(法二)由
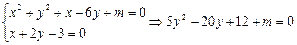 ,有
,有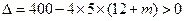 ,得m<8;(或者联立得
,得m<8;(或者联立得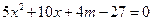 )(4分)
)(4分)(Ⅱ)设P(x1,y1), Q(x2,y2),由
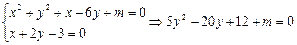
∴

由于以PQ为直径的圆过原点,∴OP⊥OQ, ∴x1x2+y1y2=0,
而x1x2=9-6(y1+y2)+4y1y2=
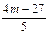 ,∴
,∴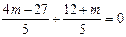 解得m=3.(8分)
解得m=3.(8分)故P(1,1), Q(-3,3),圆的方程为
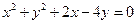 ,即
,即 .(12分)
.(12分)(法二)设过PQ的圆的方程为
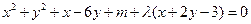
∴
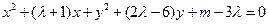 ,
,即

∵圆过原点,∴
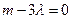 ,又以PQ为直径,则
,又以PQ为直径,则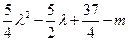 取最小值,此时
取最小值,此时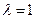 ,故m=3,圆的方程为
,故m=3,圆的方程为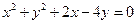 ,即
,即 .(12分)
.(12分)略

练习册系列答案
相关题目
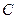 :
:
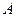 (1 , 0),
(1 , 0),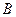 (-1 , 0),点P是圆
(-1 , 0),点P是圆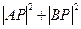 取得最小值时点
取得最小值时点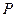 的坐标.
的坐标. 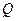 是
是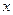 轴上的动点,
轴上的动点,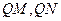 分别切圆
分别切圆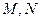 两点
两点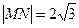 ,求直线
,求直线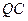 的方程;
的方程;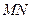 恒过一定点.
恒过一定点. 是圆
是圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与圆
与圆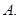 相交
相交  相切
相切  相离
相离  不能确定
不能确定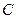 :
: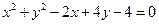 .问在圆
.问在圆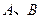 关于直线
关于直线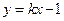 对称,且以
对称,且以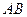 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线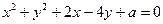 关于直线
关于直线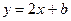 成轴对称,则
成轴对称,则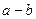 的取值范围是________.
的取值范围是________. 被圆
被圆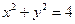 截得的弦长为2,则直线
截得的弦长为2,则直线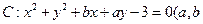 为正实数)上任意一点关于直线
为正实数)上任意一点关于直线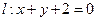 的对称点都在圆C上,则
的对称点都在圆C上,则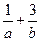 的最小值为 .
的最小值为 . 是圆
是圆 的直径,
的直径, 切圆
切圆 点,
点, 切圆
切圆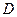 点,交
点,交 的延长线于E点,
的延长线于E点, 则
则 =____________.
=____________.