题目内容
(本小题满分10分)圆经过点A(2,-3)和B(-2,-5).
(1)若圆的面积最小,求圆的方程;
(2)若圆心在直线x-2y-3=0上,求圆的方程.
(1)若圆的面积最小,求圆的方程;
(2)若圆心在直线x-2y-3=0上,求圆的方程.
解:(1)解:要使圆的面积最小,则AB为圆的直径,所以所求圆的方程为
(x-2)(x+2)+(y+3)(y+5)=0,即x2+(y+4)2="5." …………………………………5分
(2)解法1: 因为kAB=12,AB中点为(0,-4),所以AB中垂线方程为y +4=-2x,即2x+y+4=0,解方程组
+4=-2x,即2x+y+4=0,解方程组 得
得
所以圆心为(-1,-2). 根据两点间的距离公式,得半径r=
根据两点间的距离公式,得半径r=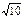 ,因此,所求的圆的方程为(x+1)2+(y+2)2="10." …………………………………10分
,因此,所求的圆的方程为(x+1)2+(y+2)2="10." …………………………………10分
解法2:所求圆的方程为 (x-a)2+(y-b)2=r2,根据已知条件得…………………………2分
(x-a)2+(y-b)2=r2,根据已知条件得…………………………2分
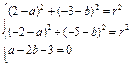
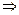
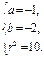 …
… ………………………………8分
………………………………8分
所以所求圆的方程为(x+1)2+(y+2)2="10." …………………………………10分
(x-2)(x+2)+(y+3)(y+5)=0,即x2+(y+4)2="5." …………………………………5分
(2)解法1: 因为kAB=12,AB中点为(0,-4),所以AB中垂线方程为y
 +4=-2x,即2x+y+4=0,解方程组
+4=-2x,即2x+y+4=0,解方程组 得
得
所以圆心为(-1,-2).
 根据两点间的距离公式,得半径r=
根据两点间的距离公式,得半径r=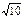 ,因此,所求的圆的方程为(x+1)2+(y+2)2="10." …………………………………10分
,因此,所求的圆的方程为(x+1)2+(y+2)2="10." …………………………………10分解法2:所求圆的方程为
 (x-a)2+(y-b)2=r2,根据已知条件得…………………………2分
(x-a)2+(y-b)2=r2,根据已知条件得…………………………2分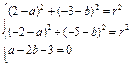
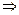
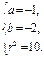 …
… ………………………………8分
………………………………8分所以所求圆的方程为(x+1)2+(y+2)2="10." …………………………………10分
略

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
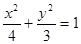 的离心率为
的离心率为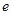 ,则过点(1,
,则过点(1,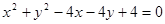 截得的最长弦所在的直线的方程是( )
截得的最长弦所在的直线的方程是( )



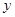 轴上,半径为1,且过点
轴上,半径为1,且过点 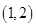 的圆的方程 ( )
的圆的方程 ( )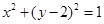 B
B 
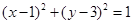 D
D 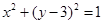
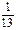
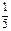
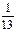

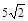
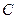 :
:
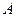 (1 , 0),
(1 , 0),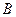 (-1 , 0),点P是圆
(-1 , 0),点P是圆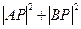 取得最小值时点
取得最小值时点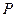 的坐标.
的坐标. 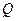 是
是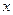 轴上的动点,
轴上的动点,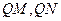 分别切圆
分别切圆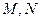 两点
两点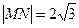 ,求直线
,求直线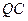 的方程;
的方程;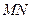 恒过一定点.
恒过一定点. 是圆
是圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与圆
与圆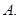 相交
相交  相切
相切  相离
相离  不能确定
不能确定 被该圆所截得的弦长为
被该圆所截得的弦长为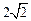 ,则圆C的标准方程为
,则圆C的标准方程为