题目内容
13.已知向量$\overrightarrow{a}$=(3cosα,1),$\overrightarrow{b}$=(-2,3sinα),且$\overrightarrow{a}⊥\overrightarrow{b}$,其中$α∈(0,\frac{π}{2})$.(Ⅰ)求sinα和cosα的值;
(Ⅱ)若5sin(α-β)=3$\sqrt{5}$cosβ,β∈(0,π),求β的值.
分析 (Ⅰ)由向量垂直得到数量积为0,得到关于α三角函数等式;
(Ⅱ)由已知条件展开得到tanβ=-1,根据角的范围取角.
解答 (Ⅰ)解:由向量$\overrightarrow{a}$=(3cosα,1),$\overrightarrow{b}$=(-2,3sinα),且$\overrightarrow{a}⊥\overrightarrow{b}$,其中$α∈(0,\frac{π}{2})$.
得-6cosα+3sinα=0…(2分)
解得tanα=2…(3分)
所以sinα=$\frac{2\sqrt{5}}{5}$,cos$α=\frac{\sqrt{5}}{5}$…(5分)
(Ⅱ)解:因为5sin(α-β)=3$\sqrt{5}$cosβ,β∈(0,π),展开得cosβ=-sinβ即tanβ=-1…(7分)
所以β=$\frac{3π}{4}$…(8分)
点评 本题考查了平面向量垂直,数量积等于0;以及三角函数的恒等变形;注意角的范围.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
3.若函数f(x)在(0,1)内有一个零点,要使零点的近似值的精确度为0.01,则需对区间(0,1)至多二等分( )
| A. | 5次 | B. | 6次 | C. | 7次 | D. | 8次 |
8.已知集合A=[-4,1),B={0,2},则A∩B为( )
| A. | {0} | B. | {2} | C. | {0,3} | D. | {x|-4<x<1} |
18.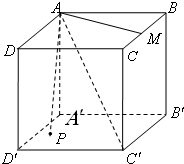 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段圆弧 | B. | 一段椭圆弧 | C. | 一段双曲线弧 | D. | 一段抛物线弧 |
2.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线都与圆(x-c)2+y2=ac(c=$\sqrt{{a}^{2}+{b}^{2}}$相切,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\frac{1+\sqrt{5}}{2}$ |
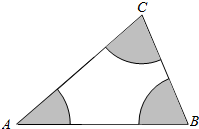 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π. 如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.
如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.