题目内容
4.已知△ABC的内角A,C满足$\frac{sinC}{sinA}$=cos(A+C),则tanC的最大值为$\frac{\sqrt{2}}{4}$.分析 由已知可得sinC=sin(A+B)=sinAcosB+cosAsinB=-sinAcosB,从而化简得tanB=-2tanA,由tanC=-tan(A+B)利用tanA表示,根据基本不等式求tanC的最大值
解答 解:由$\frac{sinC}{sinA}$=cos(A+C)=-cosB,
所以:sinC=sin(A+B)=sinAcosB+cosAsinB=-sinAcosB,
所以:cosAsinB=-2sinAcosB,
所以:tanB=-2tanA,
因为:tanC=-tan(A+B)=-$\frac{tanA+tanB}{1-tanAtanB}$=$\frac{tanA}{1+2ta{n}^{2}A}$=$\frac{1}{\frac{1}{tanA}+2tanA}$$≤\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$;当且仅当$\frac{1}{tanA}=2tanA$时等号成立.
所以tanC的最大值是$\frac{\sqrt{2}}{4}$;
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题主要考查了两角和与差的余弦函数公式、正弦函数公式、正切函数公式的应用,考查了基本不等式的应用,属于中档题.

练习册系列答案
相关题目
16.如图所示,某三棱锥的正视图、俯视图均为边长为2的正三角形,则其左视图面积为( )
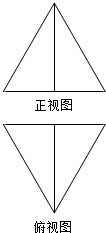

| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
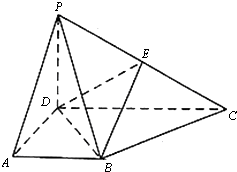 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,AD⊥AB,AD=AB=$\frac{1}{2}$CD=1,PD⊥面ABCD,PD=$\sqrt{2}$,E是PC的中点