题目内容
3．若函数f（x）在（0，1）内有一个零点，要使零点的近似值的精确度为0.01，则需对区间（0，1）至多二等分（ ）| A． | 5次 | B． | 6次 | C． | 7次 | D． | 8次 |
分析 每一次二等分都使区间的长度变为原来的一半，区间 （1，2）的长度等于1，二分6次后，区间（1，2）长度变为$\frac{1}{{2}^{6}}$=$\frac{1}{64}$＞0.01，不满足精度要求，二分7次后，区间（1，2）长度变为$\frac{1}{{2}^{7}}$=$\frac{1}{128}$＜0.01，满足精度要求，从而得到结论．
解答 解：每一次二等分都使区间的长度变为原来的一半，
∵区间 （1，2）的长度等于1，
二分6次后，区间（1，2）长度变为$\frac{1}{{2}^{6}}$=$\frac{1}{64}$＞0.01，不满足精度要求，
二分7次后，区间（1，2）长度变为$\frac{1}{{2}^{7}}$=$\frac{1}{128}$＜0.01，
故二分的次数至多有7次，
故选：C．
点评 本题主要考查用二分法求方程的近似解，注意利用每一次二等分都使区间的长度变为原来的一半，属于基础题．
练习册系列答案
相关题目
3．设函数f（x）=ex-2x，则（ ）
| A． | x=$\frac{2}{e}$为f（x）的极小值点 | B． | x=$\frac{2}{e}$为f（x）的极大值点 | ||
| C． | x=ln2为f（x）的极小值点 | D． | x=ln2为f（x）的极大值点 |
18．
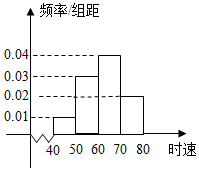已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，估计这辆汽车在这段公路时速的众数是（ ）
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，估计这辆汽车在这段公路时速的众数是（ ）| A． | 60 | B． | 65 | C． | 60.5 | D． | 70 |
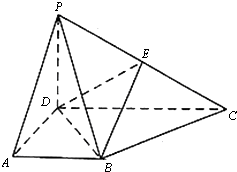已知四棱锥P-ABCD的底面是直角梯形，AB∥CD，AD⊥AB，AD=AB=$\frac{1}{2}$CD=1，PD⊥面ABCD，PD=$\sqrt{2}$，E是PC的中点