题目内容

18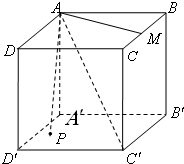．如图，正方体ABCD-A′B′C′D′中，M为BC边的中点，点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′，那么点P的轨迹是（　　）
A．一段圆弧B．一段椭圆弧C．一段双曲线弧D．一段抛物线弧

分析 由题意知点P在以AC′为轴，A为顶点，AM为母线的圆锥上运动，同时AM∥底面A′B′C′D′，从而判断．

解答 解：∵∠MAC′=∠PAC′，
∴点P在以AC′为轴，A为顶点，AM为母线的圆锥上运动，
又∵AM∥底面A′B′C′D′，
且点P在底面A′B′C′D′上运动；
∴点P的轨迹是一段抛物线弧．
故选D．

点评 本题考查了圆锥曲线的几何定义应用，属于基础题．

练习册系列答案
相关题目
8．若正方体ABCD-A1B1C1D1中，E，F分别为AB，CC1的中点，则异面直线EF和A1C1所成角的大小是30°．
9．若点（1，-2）与点（-2，0）在直线x+y+a=0的两侧，同时点（1，-2）和点（-1，-4）都在不等式bx+y+2＜0所表示的区域内，求a+b与a-b的取值范围．
6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的右焦点为F（$\sqrt{3}$，0），上下两个顶点与点F恰好是正三角形的三个顶点．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过原点O的直线l与椭圆交于A，B两点，如果△FAB为直角三角形，求直线l的方程．
13．已知向量$\overrightarrow{a}$=（3cosα，1），$\overrightarrow{b}$=（-2，3sinα），且$\overrightarrow{a}⊥\overrightarrow{b}$，其中$α∈（0，\frac{π}{2}）$．
（Ⅰ）求sinα和cosα的值；
（Ⅱ）若5sin（α-β）=3$\sqrt{5}$cosβ，β∈（0，π），求β的值．
3．下列函数中，在其定义域内，既是奇函数又是减函数的是（　　）
A．f（x）=-x3B．f（x）=$\sqrt{-x}$C．f（x）=-tanxD．f（x）=$\frac{1}{x}$
10．如图，已知AD是△ABC的对角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连结FB，FC．
（1）求证：FB=FC；
（2）若FA=2，AD=6，求FB的长．
7．已知9a=3，lgx=a 则x=$\sqrt{10}$．
8．已知直线l过点（0，-1），且直线y=-x+2垂直，则直线l的方程为x-y-1=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网