题目内容
1.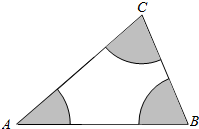 如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
如图所示,分别以A,B,C为圆心,在△ABC内作半径为2的扇形(图中的阴影部分),在△ABC内任取一点P,如果点P落在阴影内的概率为$\frac{1}{3}$,那么△ABC的面积是6π.
分析 由题意知本题是一个几何概型,先试验发生包含的所有事件是三角形的面积S,然后求出阴影部分的面积,代入几何概率的计算公式即可求解.
解答 解:由题意知本题是一个几何概型,
∵试验发生包含的所有事件是直角三角形的面积S,
阴影部分的面积S1=$\frac{1}{2}$π22=2π.
点P落在区域M内的概率为P=$\frac{2π}{S}$=$\frac{1}{3}$.
故S=6π,
故答案为:6π.
点评 本题考查几何概型,且把几何概型同几何图形的面积结合起来,几何概型和古典概型是高中必修中学习的,高考时常以选择和填空出现,有时文科会考这种类型的解答.

练习册系列答案
相关题目
16.如图所示,某三棱锥的正视图、俯视图均为边长为2的正三角形,则其左视图面积为( )
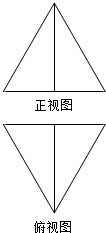

| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
如图,已知AD是△ABC的对角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.