题目内容
【题目】已知向量 
=（1，2）， 
=（2，﹣3）．
（1）若 
垂直，求λ的值；
（2）求向量 在 方向上的投影．
【答案】
（1）解： 
，
由于 
与 
垂直，
∴2λ+1+2（2﹣3λ）=0，
∴ 
（2）解：设向量 与 
的夹角为θ，向量 在 方向上的投影为 
，
∴ 
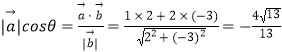
【解析】1、由向量的线性运算可得的坐标为( 2 λ + 1 ， 2 3 λ ) ，再根据向量垂直的坐标表示可得到结果。
2、根据数量积的计算公式求得 向量 在 方向上的投影为 | | c o s θ ,利用数量积的公式求得。
【考点精析】认真审题，首先需要了解数量积判断两个平面向量的垂直关系(若平面
的法向量为
，平面
的法向量为
，要证
，只需证
，即证
;即：两平面垂直
两平面的法向量垂直)．
练习册系列答案
相关题目
【题目】一个生物研究性学习小组，为了研究平均气温与一天内某豆类胚芽生长之间的关系，他们分别记录了4月6日至4月11日的平均气温x（℃）与该豆类胚芽一天生长的长度y（mm），得到如下数据：
日期 | 4月6日 | 4月7日 | 4月8日 | 4月9日 | 4月10日 | 4月11日 |
平均气温x（℃） | 10 | 11 | 13 | 12 | 8 | 6 |
一天生长的长度y（mm） | 22 | 25 | 29 | 26 | 16 | 12 |
该小组的研究方案是：先从这六组数据中选取6日和11日的两组数据作为检验数据，用剩下的4组数据即：7日至10日的四组数据求出线性回归方程．
（1）请按研究方案求出y关于x的线性回归方程 
= 
x+ 
；
（2）用6日和11日的两组数据作为检验数据，并判断该小组所得线性回归方程是否理想．（若由线性回归方程得到的估计数据与所选的检验数据的误差不超过1mm，则认为该方程是理想的）
参考公式： 
．
