Question

【题目】已知椭圆 的左、右焦点分别为 ，其离心率 ，点 为椭圆上的一个动点，△ 面积的最大值为 .
（1）求椭圆的标准方程；
（2）若 是椭圆上不重合的四个点， 与 相交于点 ， 求 的取值范围.

Answer 1

【答案】
（1）解：由题意得，当点 是椭圆的上、下顶点时，△ 的面积取最大值，

此时 所以 因为 所以 ， ,

所以椭圆方程为

（2）解：由（1）得椭圆方程为 ，则 的坐标为 ，

因为 ，所以 .

①当直线 与 中有一条直线斜率不存在时，易得 .

②当直线 斜率 存在且 时，则其方程为 ，设 ，

则点 、 的坐标是方程组 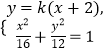的两组解，

所以

所以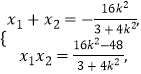

所以 .

直线 的方程为 .

同理可得 ,

，

令 ，则 ，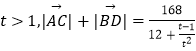

因为 ，所以 ， ，

所以 ，

所以

【解析】(1)由题意可知当点P为椭圆的上下顶点时，三角形的面积最大再根据椭圆的离心率可得到关于a与c的方程解出方程即可求出其值，进而可得到椭圆的方程。(2)首先求出AC、BD中有一条直线不存在斜率时,当直线AC存在斜率且不为零时，由点斜式写出直线的方程再联立椭圆的方程消元得到关于x的一元二次方程，由韦达定理求出两根之和与两根之积代入到弦长公式求得的代数式，把k换为即可得到所以用k表示出结果的代数式，再由整体思想设出t=k2+1根据t的范围，结合代数式的几何意义得到取值范围。