题目内容
【题目】已知函数 
（1）求函数f（x）在 
上的最大值与最小值；
（2）已知 
，x0∈（ 
， 
），求cos4x0的值．
【答案】
（1）解：函数 
化简可得：3 
+ 
sin2x﹣ 
= 
﹣ cos2x× 
+ × 
sin2x+ sin2x﹣ 
﹣ cos2x
= 
sin2x﹣cos2x+ 
=2sin（2x﹣ 
）+ ．
∵x∈ 
上，
∴2x﹣ ∈[ 
， 
]．
∴sin（2x﹣ ）∈[ 
，1]．
函数f（x）在 上的最大值为 
，最小值为 ．
（2）解：∵ 
，即2sin（4x0﹣ ）+ = 
sin（4x0﹣ ）= 
∵x0∈（ ， 
），
4x0﹣ ∈[ 
，π]，
∴cos（4x0﹣ ）= 
．
cos4x0=cos[4x0﹣ ） 
]=cos（4x0﹣ ）cos ﹣sin（4x0﹣ ）sin = × 
﹣ 
= 
．
【解析】（1）根据二倍角和两角差的正弦公式将f（x）化简为f（x）=Asin（ωx+φ）的形式，结合正弦函数的图象和性质可得到在给定区间的最值，（2）由题意代入找得到sin（4x0﹣ ），cos（4x0﹣ ）的值，根据cos4x0=cos[（4x0﹣ ） + ]，由两角和的余弦公式展开代值可求得.
练习册系列答案
相关题目
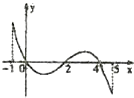
【题目】已知函数f（x）的定义域[﹣1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示
x | ﹣1 | 0 | 2 | 4 | 5 |
F（x） | 1 | 2 | 1.5 | 2 | 1 |
下列关于函数f（x）的命题；
①函数f（x）的值域为[1，2]；
②函数f（x）在[0，2]上是减函数
③如果当x∈[﹣1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）﹣a最多有4个零点．
其中正确命题的序号是 ． 
