题目内容
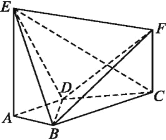
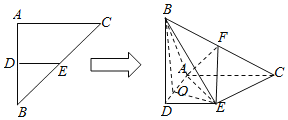
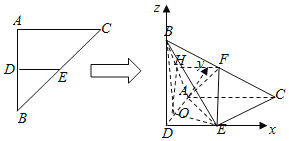
【题目】在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B﹣ADEC,且F为棱BC中点,BA![]() .
.
(1)求证:EF⊥平面BAC;
(2)在线段AD上是否存在一点Q,使得AF∥平面BEQ?若存在,求二面角Q﹣BE﹣A的余弦值,若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]()
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,在等腰
,在等腰![]() 中,由已知可得
中,由已知可得![]() ,则
,则![]() ,由线面垂直的判定可得
,由线面垂直的判定可得![]() 平面
平面![]() ,进一步得到
,进一步得到![]() 平面
平面![]() ,则
,则![]() ,可得
,可得![]() 平面
平面![]() ,然后证明
,然后证明![]() 是平行四边形,得
是平行四边形,得![]() ,从而得到
,从而得到![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点建立如图所示空间直角坐标系
为原点建立如图所示空间直角坐标系![]() .求出
.求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的坐标,设
的坐标,设![]() ,
,![]() ,
,![]() ,求出平面
,求出平面![]() 的法向量
的法向量![]() ,由
,由![]() 求得
求得![]() ,即线段
,即线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,再求出平面
,再求出平面![]() 的法向量为
的法向量为![]() ,由两法向量所成角的余弦值可得二面角
,由两法向量所成角的余弦值可得二面角![]() 的余弦值.
的余弦值.
(1)证明:取![]() 中点
中点![]() ,连结
,连结![]() 、
、![]() ,在等腰
,在等腰![]() 中,
中,
![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,
的中点,![]() ,
,
又![]() 翻折后
翻折后![]() ,
,![]() 翻折后
翻折后![]() ,且
,且![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,
,
![]() 翻折后
翻折后![]() ,
,![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() ,则
,则![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
又![]() ,
,![]() ,且
,且![]() ,
,
![]() 是平行四边形,则
是平行四边形,则![]() ,
,
![]() 平面
平面![]() ;
;
(2)以![]() 为原点建立如图所示空间直角坐标系
为原点建立如图所示空间直角坐标系![]() .则
.则![]() ,1,
,1,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,1,
,1,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,则由
,则由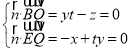 ,取
,取![]() ,则
,则![]() ,1,
,1,![]() ,
,
要使![]() 平面
平面![]() ,则须
,则须![]() ,
,
![]()
![]() ,即线段
,即线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,则由
,则由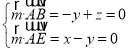 ,取
,取![]() ,则
,则![]() ,1,
,1,![]() ,
,
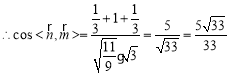 ,
,
![]() 二面角
二面角![]() 为锐二面角,
为锐二面角,![]() 其余弦值为
其余弦值为![]() ,
,
即线段![]() 上存在一点
上存在一点![]() (点
(点![]() 是线段
是线段![]() 上的靠近点
上的靠近点![]() 的一个三等分点),
的一个三等分点),
使得![]() 平面
平面![]() ,此时二面角
,此时二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目