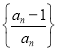
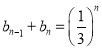题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,M是椭圆C的上顶点,
,M是椭圆C的上顶点,![]() ,F2是椭圆C的焦点,
,F2是椭圆C的焦点,![]() 的周长是6.
的周长是6.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过动点P(1,t)作直线交椭圆C于A,B两点,且|PA|=|PB|,过P作直线l,使l与直线AB垂直,证明:直线l恒过定点,并求此定点的坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)由题得到关于a,b,c的方程组,解方程组即得椭圆C的标准方程;(Ⅱ)当直线AB斜率存在,设AB的直线方程为![]() ,进一步求出直线的方程为
,进一步求出直线的方程为![]() ,
,
所以直线![]() 恒过定点
恒过定点![]() .当直线
.当直线![]() 斜率不存在时,直线
斜率不存在时,直线![]() 的方程为
的方程为![]() ,此时直线
,此时直线![]() 为
为![]() 轴,也过
轴,也过![]() .综上所述直线
.综上所述直线![]() 恒过点
恒过点![]() .
.
解:(Ⅰ)由于![]() 是椭圆
是椭圆![]() 的上顶点,由题意得
的上顶点,由题意得![]() ,
,
又椭圆离心率为![]() ,即
,即![]() ,
,
解得![]() ,
,![]() ,
,
又![]() ,
,
所以椭圆![]() 的标准方程
的标准方程![]() 。
。
(Ⅱ)当直线AB斜率存在,设AB的直线方程为![]() ,
,
联立![]() ,得
,得
![]() ,
,
由题意,![]() ,
,
设![]() ,
,
则![]() ,
,
因为![]() ,所以
,所以![]() 是
是![]() 的中点.
的中点.
即![]() ,得
,得![]() ,
,
![]() ①
①
又![]() ,l的斜率为
,l的斜率为![]() ,
,
直线![]() 的方程为
的方程为![]() ②
②
把①代入②可得:![]()
所以直线![]() 恒过定点
恒过定点![]() .
.
当直线![]() 斜率不存在时,直线
斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
此时直线![]() 为
为![]() 轴,也过
轴,也过![]() .
.
综上所述直线![]() 恒过点
恒过点![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤