题目内容
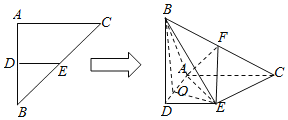
【题目】如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB=AD=1,AE=BC=2.
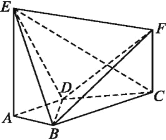
(1)求证:BF∥平面ADE;
(2)若二面角E-BD-F的余弦值为![]() ,求线段CF的长.
,求线段CF的长.
【答案】(1)证明见解析(2)![]()
【解析】
(1)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,求出相应点的坐标,设
轴建立空间直角坐标系,求出相应点的坐标,设![]() ,然后证明
,然后证明![]() 的方向向量和面
的方向向量和面![]() 的法向量数量积为0即可;
的法向量数量积为0即可;
(2)分别求出平面![]() 和平面
和平面![]() 的法向量,由两平面法向量所成角的余弦值为
的法向量,由两平面法向量所成角的余弦值为![]() 列式求线段
列式求线段![]() 的长.
的长.
(1)证明:以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,可得
轴建立空间直角坐标系,可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]() ,
,
则![]() 是平面
是平面![]() 的法向量,
的法向量,
又![]() ,可得
,可得![]() ,
,
又∵直线![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
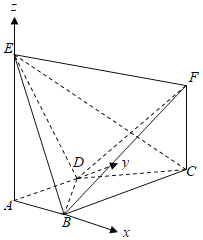
(2)设![]() 为平面
为平面![]() 的法向量,
的法向量,
则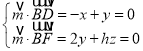 ,取
,取![]() ,可得
,可得![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则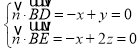 ,令
,令![]() ,得
,得![]() ,
,
由题意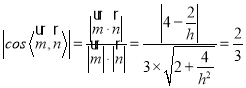 ,
,
解得![]() ,经检验,符合题意.
,经检验,符合题意.
∴线段![]() 的长为
的长为![]() .
.

练习册系列答案
相关题目
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤