Question

【题目】已知点Q是圆上的动点，点，若线段QN的垂直平分线MQ于点P.

(I)求动点P的轨迹E的方程

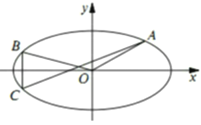
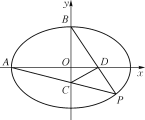
(II)若A是轨迹E的左顶点，过点D（-3，8）的直线l与轨迹E交于B，C两点，求证：直线AB、AC的斜率之和为定值.

Answer 1

【答案】(Ⅰ) (Ⅱ)见证明

【解析】

（Ⅰ）线段的垂直平分线交于点P，所以，则为定值，所以P的轨迹是以为焦点的椭圆，结合题中数据求出椭圆方程即可；（Ⅱ）设出直线方程，联立椭圆方程得到韦达定理，写出化简可得定值.

解：（Ⅰ）由题可知，线段的垂直平分线交于点P，

所以，则，

所以P的轨迹是以为焦点的椭圆，

设该椭圆方程为，

则，所以，

可得动点P的轨迹E的方程为.

（Ⅱ）由（Ⅰ）可得，过点D的直线斜率存在且不为0，

故可设l的方程为，，

由得，

而

由于直线过点，所以，

所以（即为定值）