题目内容
1．若函数f（x）=$\frac{{e}^{x}-1}{{e}^{x}+1}$，对任意的m∈[-2，2]，f（mx-3）+f（x）＜0恒成立，则x的取值范围是（-3，1）．分析 由题意知原函数在R上单调递增，且为奇函数，由f（mx-3）+f（x）＜0恒成立得mx-3＜-x⇒xm+x-3＜0，对所有m∈[-2，2]恒成立，然后构造函数f（m）=xm+x-2，利用该函数的单调性可解得x的范围．
解答 解：函数f（x）=$\frac{{e}^{x}-1}{{e}^{x}+1}$，
即为f（x）=1-$\frac{2}{{e}^{x}+1}$，
则函数在R上单调递增，
又f（-x）=$\frac{{e}^{-x}-1}{{e}^{-x}+1}$=$\frac{1-{e}^{x}}{1+{e}^{x}}$=-f（x），
则为奇函数，
故f（mx-3）+f（x）＜0，
则f（mx-3）＜-f（x）=f（-x），
此时应有mx-3＜-x，
即xm+x-3＜0，对所有m∈[-2，2]恒成立，
令g（m）=xm+x-3，
此时只需$\left\{\begin{array}{l}{g（-2）=-x-3＜0}\\{g（2）=3x-3＜0}\end{array}\right.$即可，
解之得-3＜x＜1，
则x的取值范围为（-3，1）．
故答案为：（-3，1）．
点评 本题考查了函数的单调性与奇偶性的综合应用，在解决不等式恒成立问题时注意变换主元的方法，是个中档题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
12．设函数f（x）=3sin（ωx+$\frac{π}{6}$）（ω＞0）的周期是π，则（ ）
| A． | f（x）的图象过点（0，$\frac{1}{2}$） | |
| B． | f（x）在[$\frac{π}{12}$，$\frac{2π}{3}$]上是减函数 | |
| C． | f（x）的一个对称中心是（$\frac{5π}{12}$，0） | |
| D． | 将f（x）的图象向右平移$\frac{π}{6}$个单位得到函数y=3sinωx的图象 |
9．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{2}$，且$\overrightarrow{b}$•（2$\overrightarrow{a}$+$\overrightarrow{b}$）=1，则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值是（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{\sqrt{2}}{3}$ | C． | -$\frac{\sqrt{2}}{4}$ | D． | $\frac{1}{3}$ |
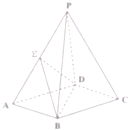如图，在四棱锥P-ABCD中，底面ABCD是矩形，E是棱PA的中点，PD⊥BC，求证：