题目内容
16．
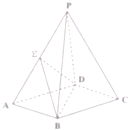如图，在四棱锥P-ABCD中，底面ABCD是矩形，E是棱PA的中点，PD⊥BC，求证：（Ⅰ）PC∥平面BED；
（Ⅱ）BC⊥PC．
分析 （Ⅰ）欲证明PC∥平面BED，只需根据三角形中位线定理推知OE∥PC即可；
（Ⅱ）通过BC⊥平面PDC来证得结论．
解答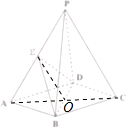 
证明：（Ⅰ）连接AC交BD于点O，连接OE．
在矩形ABCD中，AO=OC．
因为AE=EP，
所以OE∥PC．
因为PC?平面BDE，OE?平面BDE，
所以PC∥平面BDE．
（Ⅱ）在矩形ABCD中，BC⊥CD．
因为PD⊥BC，CD∩PE=D，PD?平面PDC，DC?平面PDC，
所以BC⊥平面PDC．
因为PC?平面PDC，
所以BC⊥BC．
点评 本题考查了空间中直线与直线之间的位置关系，直线与平面平行的判定．判定的关键是先找到到线线平行，线线垂直．
练习册系列答案
名校课堂系列答案
相关题目
6．已知tanα=4，则$\frac{{1+cos2α+8{{sin}^2}α}}{sin2α}$的值为（ ）
| A． | 18 | B． | $\frac{1}{4}$ | C． | 16 | D． | $\frac{65}{4}$ |
11．已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上一点到两焦点F1，F2的距离之积是m，则m取最大值时，点P的坐标为（ ）
| A． | （$\frac{5}{2}$，$\frac{3\sqrt{3}}{2}$）或（$\frac{5}{2}$，-$\frac{3\sqrt{3}}{2}$） | B． | （5，0）或（-5，0） | ||
| C． | （$\frac{5\sqrt{3}}{2}$，$\frac{3}{2}$）或（-$\frac{5\sqrt{3}}{2}$，-$\frac{3}{2}$） | D． | （0，3）或（0，-3） |