题目内容
12.设函数f(x)=3sin(ωx+$\frac{π}{6}$)(ω>0)的周期是π,则( )| A. | f(x)的图象过点(0,$\frac{1}{2}$) | |
| B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | |
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | |
| D. | 将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数y=3sinωx的图象 |
分析 根据周期函数的定义可以求得ω=2,由此可以求得该函数解析式,然后根据解析式对下列选项进行一一计算即可.
解答 解:∵函数f(x)=3sin(ωx+$\frac{π}{6}$)(ω>0)的周期是π,
∴2π÷ω=π,则ω=2.
∴该函数是:f(x)=3sin(2x+$\frac{π}{6}$).
A、当x=0时,f(x)=3sin$\frac{π}{6}$=3×$\frac{1}{2}$=$\frac{3}{2}$,即该函数经过点(0,$\frac{3}{2}$),故本选项错误;
B、由正弦函数的单调递增区间为[2kπ+$\frac{π}{2}$,2kπ+π],(k∈Z),
得到2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3}{2}$π,(k∈Z),
解得:kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,(k∈Z),
∴f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是增函数,故本选项错误;
C、f(x)的对称中心是(kπ,0),则2x+$\frac{π}{6}$=kπ,
解得x=$\frac{kπ}{2}$-$\frac{π}{12}$.
当k=1时,x=$\frac{5π}{12}$,即f(x)的一个对称中心是($\frac{5π}{12}$,0),故本选项正确;
D、将f(x)的图象向右平移$\frac{π}{12}$个单位得到函数y=3sinωx的图象,故本选项错误;
故选:C.
点评 此题考查了三角函数的周期性及其求法,以及正弦函数的单调性,熟练掌握三角函数的周期公式及正弦函数的单调性是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.方程$\sqrt{{x}^{2}+(y+3)^{2}}$+$\sqrt{{x}^{2}+(y-3)^{2}}$=10,化简的结果是( )
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1 |
17.5人排成一排,甲只能排在第一个或第二两个位置,乙只能排在第二或第三两个位置,不同的排法共有( )
| A. | 12种 | B. | 16种 | C. | 18种 | D. | 24种 |
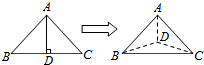 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折