题目内容
10.求过点(1,1)且与y=x3相切的直线方程.分析 设切点为(x0,y0),根据解析式求出导数、y0,由导数的几何意义求出切线的斜率,由点斜式方程求出切线方程,把点(1,1)代入切线方程通过因式分解求出x,代入切线方程化简即可.
解答 解:设切点为(x0,y0),由题意得y=3x2,y0=x03,
则切线的斜率k=3x02,
∴切线方程是:y-x03=3x02(x-x0),①
∵切线过过点(1,1),∴1-x03=3x02(1-x0),
化简得,2x03-3x02+1=0,
2(x03-1)-3(x02-1)=0,
则(x0-1)(2x02-x0-1)=0,
解得x0=1或x0=$\frac{1}{2}$,代入①得:3x-y-2=0或3x-4y+1=0,
∴切线方程为3x-y-2=0或3x-4y+1=0.
点评 本题考查了导数的几何意义,即点P处的切线的斜率是该点出的导数值,以及切点在曲线上和切线上的应用,注意在某点处的切线和过某点的切线的区别,考查化简、计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在△ABC中,内角A,B,C所对的边分别是a,b,c,B=60°,a+c=1,则b的取值范围为( )
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{1}{4}$,1) | C. | [$\frac{1}{4}$,$\frac{1}{2}$) | D. | (0,1) |
2.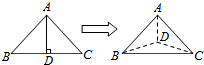 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
19.若θ是△ABC的一个内角,且sinθcosθ=$\frac{1}{8}$,则sinθ+cosθ=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
19.执行如图的程序框图,如果输入的N=10,那么输出的S=( )


| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | ||
| C. | 1+$\frac{1}{2×1}$+$\frac{1}{3×2×1}$+…+$\frac{1}{10×9×…×3×2×1}$ | D. | 1+$\frac{1}{2×1}$+$\frac{1}{3×2×1}$+…+$\frac{1}{11×10×…×3×2×1}$ |