题目内容
11.数列{an}的前n项和为Sn,若${a_n}=\frac{1}{{n({n+2})}}$,则S10等于$\frac{175}{264}$.分析 通过裂项可得an=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),并项相消计算即可.
解答 解:∵${a_n}=\frac{1}{{n({n+2})}}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴S10=$\frac{1}{2}$[(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{9}$+$\frac{1}{10}$)-($\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+…+$\frac{1}{11}$+$\frac{1}{12}$)]
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{11}$-$\frac{1}{12}$)
=$\frac{1}{2}$•$\frac{11×12+11×6-12-11}{11×12}$
=$\frac{175}{264}$,
故答案为:$\frac{175}{264}$.
点评 本题考查求数列的和,注意解题方法的积累,属于基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
2. 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
19.若θ是△ABC的一个内角,且sinθcosθ=$\frac{1}{8}$,则sinθ+cosθ=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $-\frac{{\sqrt{5}}}{2}$ |
16.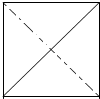 棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )
棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )
 棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )
棱长相等的三棱锥A-BCD的俯视图是边长为2的正方形,如图所示,若该几何体的另一个棱长都相等的三棱锥A′-B′C′D′纸盒内可以任意转动,则三棱锥A′-B′C′D′的棱长的最小值为( )| A. | 3$\sqrt{6}$ | B. | 8 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
19.执行如图的程序框图,如果输入的N=10,那么输出的S=( )
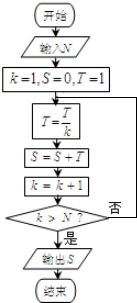

| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{10}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{11}$ | ||
| C. | 1+$\frac{1}{2×1}$+$\frac{1}{3×2×1}$+…+$\frac{1}{10×9×…×3×2×1}$ | D. | 1+$\frac{1}{2×1}$+$\frac{1}{3×2×1}$+…+$\frac{1}{11×10×…×3×2×1}$ |