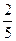题目内容
已知椭圆4x2+4by2=3与直线x+y-1=0相交于不同的两点,则实数b的范围是___________.
(0,1)∪(1,3)
联立方程组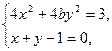
消去y得4(1+b)x2-8bx+4b-3="0. " (*)
∵直线x+y-1=0与椭圆4x2+4by2=3相交于两个不同的点,
∴(*)有两个不同的实数解,即(-8b)2-4×4(1+b)(4b-3)>0.解得b<3.又方程4x2+4by2=3为椭圆方程,
∴b>0且b≠1.
故b的取值范围为(0,1)∪(1,3).
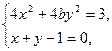
消去y得4(1+b)x2-8bx+4b-3="0. " (*)
∵直线x+y-1=0与椭圆4x2+4by2=3相交于两个不同的点,
∴(*)有两个不同的实数解,即(-8b)2-4×4(1+b)(4b-3)>0.解得b<3.又方程4x2+4by2=3为椭圆方程,
∴b>0且b≠1.
故b的取值范围为(0,1)∪(1,3).

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
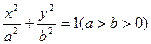 的左右焦点分别为
的左右焦点分别为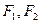 ,
,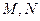 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且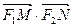 =0.
=0.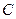 是以
是以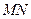 为直径的圆,试判断原点
为直径的圆,试判断原点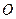 与圆
与圆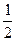 ,
,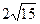 ,求椭圆的方程
,求椭圆的方程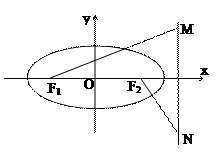
 到两个定点
到两个定点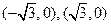 的距离的和等于4.
的距离的和等于4. 的方程;
的方程;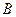 在曲线
在曲线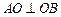 ,试求
,试求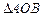 面积的最大值和最小值.
面积的最大值和最小值. a.
a.
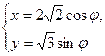 (φ为参数)上一点M与原点的连线与x轴正方向所成角为
(φ为参数)上一点M与原点的连线与x轴正方向所成角为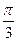 ,求点M的坐标.
,求点M的坐标. +
+ =1,若它的一条弦AB被M(1,1)平分,则AB所在的直线方程为________.
=1,若它的一条弦AB被M(1,1)平分,则AB所在的直线方程为________.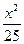 +
+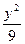 =1上一点P到两焦点距离之积为m,则m最大时求P点坐标.
=1上一点P到两焦点距离之积为m,则m最大时求P点坐标. +
+  =1(x≠±2)
=1(x≠±2) +
+ =1(y≠±2)
=1(y≠±2)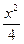 +y2=1相交于A、B两点,则|AB|的最大值是( )
+y2=1相交于A、B两点,则|AB|的最大值是( )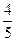
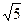 C.
C.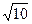 D.
D.