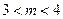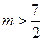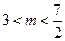题目内容
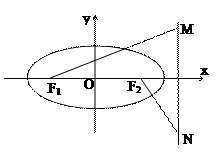
如图,椭圆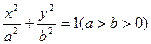 的左右焦点分别为
的左右焦点分别为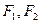 ,
,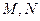 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且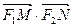 =0.
=0.
(1)设圆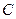 是以
是以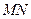 为直径的圆,试判断原点
为直径的圆,试判断原点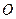 与圆
与圆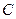 的位置关系
的位置关系
(2)设椭圆的离心率为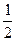 ,
,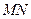 的最小值为
的最小值为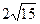 ,求椭圆的方程
,求椭圆的方程
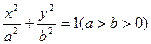 的左右焦点分别为
的左右焦点分别为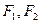 ,
,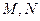 是椭圆右准线上的两个动点,且
是椭圆右准线上的两个动点,且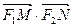 =0.
=0.(1)设圆
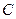 是以
是以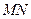 为直径的圆,试判断原点
为直径的圆,试判断原点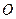 与圆
与圆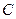 的位置关系
的位置关系(2)设椭圆的离心率为
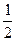 ,
,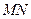 的最小值为
的最小值为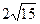 ,求椭圆的方程
,求椭圆的方程
(1)点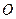 在圆
在圆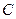 外部(2)
外部(2)
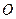 在圆
在圆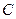 外部(2)
外部(2)
(1)设椭圆 的焦距为
的焦距为
则其右准线方成为
设
则
因为 ,所以
,所以
即 ,所以
,所以 MON为锐角
MON为锐角
点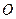 在圆
在圆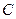 外部 -------------------------5分
外部 -------------------------5分
(2)∵椭圆的离心率为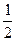 ,∴
,∴
于是 ,且
,且
 ----------------------------------10分
----------------------------------10分
当且仅当 或
或 时取等号
时取等号
所以 ,于是
,于是
故所求的椭圆方程为 ----------————————12分
----------————————12分
 的焦距为
的焦距为
则其右准线方成为

设

则

因为
 ,所以
,所以
即
 ,所以
,所以 MON为锐角
MON为锐角 点
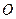 在圆
在圆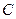 外部 -------------------------5分
外部 -------------------------5分(2)∵椭圆的离心率为
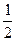 ,∴
,∴
于是
 ,且
,且
 ----------------------------------10分
----------------------------------10分当且仅当
 或
或 时取等号
时取等号所以
 ,于是
,于是
故所求的椭圆方程为
 ----------————————12分
----------————————12分
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
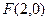 ,且两条准线间的距离为
,且两条准线间的距离为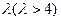 。
。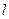 ,使点F关于直线
,使点F关于直线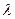 的取值范围。
的取值范围。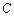 的方程为
的方程为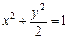 ,点
,点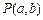 的坐标满足
的坐标满足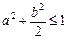
 过点
过点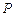 的直线
的直线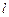 与椭圆交于
与椭圆交于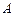 、
、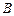 两点,点
两点,点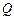 为线段
为线段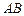 的中点,求:
的中点,求: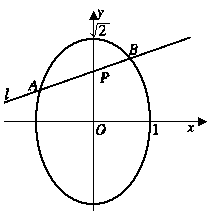
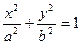 (a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.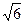 , 求椭圆方程.
, 求椭圆方程.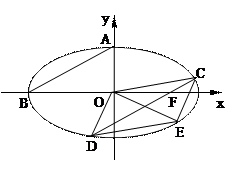
 截圆柱体,截口是一条封闭曲线,且截面与底面所成的
截圆柱体,截口是一条封闭曲线,且截面与底面所成的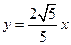 和
和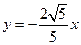 上的两个动点,并且
上的两个动点,并且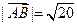 ,动点P满足
,动点P满足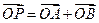 .记动点P的轨迹为C.
.记动点P的轨迹为C.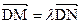 ,求实数
,求实数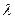 的取值范围.
的取值范围.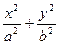 =1(
=1(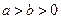 )的离心率为
)的离心率为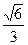 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为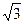 .
. 的方程;
的方程;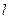 与椭圆
与椭圆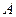 、
、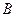 两点,坐标原点
两点,坐标原点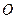 到直线
到直线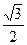 ,求△
,求△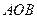 面积的最大值.
面积的最大值.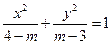 表示焦点在
表示焦点在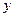 轴上的椭圆,则
轴上的椭圆,则 的取值范围是( )
的取值范围是( )