题目内容
椭圆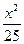 +
+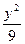 =1上一点P到两焦点距离之积为m,则m最大时求P点坐标.
=1上一点P到两焦点距离之积为m,则m最大时求P点坐标.
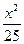 +
+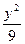 =1上一点P到两焦点距离之积为m,则m最大时求P点坐标.
=1上一点P到两焦点距离之积为m,则m最大时求P点坐标.P点的坐标为(0,±3).
设P(x0,y0),则|PF1|=a+ex0=5+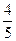 x0,|PF2|=a-ex0=5-
x0,|PF2|=a-ex0=5-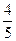 x0,∴m=|PF1|·|PF2|=25-
x0,∴m=|PF1|·|PF2|=25-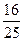 x02.
x02.
又x0∈[-5,5],故当x0=0时,mmax=25-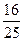 ×02=25,此时y0=±3.故P点的坐标为(0,±3).
×02=25,此时y0=±3.故P点的坐标为(0,±3).
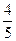 x0,|PF2|=a-ex0=5-
x0,|PF2|=a-ex0=5-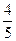 x0,∴m=|PF1|·|PF2|=25-
x0,∴m=|PF1|·|PF2|=25-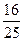 x02.
x02.又x0∈[-5,5],故当x0=0时,mmax=25-
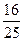 ×02=25,此时y0=±3.故P点的坐标为(0,±3).
×02=25,此时y0=±3.故P点的坐标为(0,±3).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
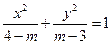 表示焦点在
表示焦点在 轴上的椭圆,则
轴上的椭圆,则 的取值范围是( )
的取值范围是( )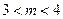
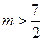
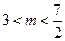

 ,且和直线3x+2
,且和直线3x+2 y-16=0相切,求椭圆方程.
y-16=0相切,求椭圆方程. +y2=1(y≥0),求
+y2=1(y≥0),求 的最大值、最小值.
的最大值、最小值.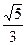 ,一条准线为y=3.
,一条准线为y=3. ,求∠ABF.
,求∠ABF.
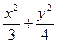 ="1"
="1"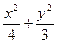 =1
=1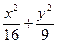 ="1"
="1"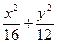 =1
=1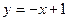 与椭圆
与椭圆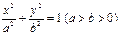 相交于A、B两点.。
相交于A、B两点.。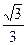 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;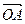 与向量
与向量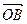 互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.
互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.