题目内容

2．不等式|x+3|＜4的解是（　　）
A．{x|x＜-7}B．{x|-7＜x＜1}C．{x|x＞1}D．{x|x＜-7或x＞1}

分析 由题意可得可得-4＜x+3＜4，由此求得x的范围．

解答 解：由不等式|x+3|＜4，可得-4＜x+3＜4，求得-7＜x＜1，
故选：B．

点评 本题主要考查绝对值不等式的解法，体现了转化的数学思想，属于基础题．

练习册系列答案
相关题目
12．设三次函数f（x）=ax3+bx2+cx+1的导函数f′（x）=3ax（x-1），且a＞2，则函数f（x）的零点个数为（　　）
A．0B．1C．2D．3
13．已知$\frac{\overline z}{i}$=2-i，则在复平面内，复数z对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
10．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x≤0}\\{1-3x，x＞0}\end{array}\right.$，若f（2a2-3）＞f（5a），则实数a的取值范围是（-$\frac{1}{2}$，3）．
17．设O、A、B、C为平面上四个点，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$且$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$，$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$=$\overrightarrow{c}$•$\overrightarrow{a}$=-1，则|$\overrightarrow{a}$|+|$\overrightarrow{b}$|+|$\overrightarrow{c}$|=$3\sqrt{2}$．
4．已知椭圆以坐标原点为中心，坐标轴为对称轴，以抛物线y2=16x的焦点为其中一个焦点，以双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的焦点为顶点．
（1）求椭圆的标准方程；
（2）已知点A（-1，0），B（1，0），且C，D分别为椭圆的上顶点和右顶点，点M是线段CD上的动点，求$\overrightarrow{AM}$•$\overrightarrow{BM}$的最小值；
（3）若E，F是椭圆上关于原点对称的两点，P是椭圆上任意一点，则当直线PE，PF的斜率都存在，并记为kPE，kPF时，kPE•kPF是否为定值，若时求出这个定值，若不是，请说明理由．
11．数列{an}中，若Sn=n2an，a1=$\frac{1}{2}$，则an=$\frac{1}{n（n+1）}$．
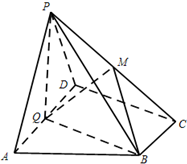8．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，$BC=\frac{1}{2}AD=1$，$CD=\sqrt{3}$．
（1）求证：平面MQB⊥平面PAD；
（2）若满足BM⊥PC，求异面直线AP与BM所成角的余弦值；
（3）若二面角M-BQ-C大小为30°，求QM的长．
9．已知公差不为0的等差数列{an}满足a1，a3，a4成等比数列，Sn为{an}的前n项和，则$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$的值为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网