题目内容
12.设三次函数f(x)=ax3+bx2+cx+1的导函数f′(x)=3ax(x-1),且a>2,则函数f(x)的零点个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据导数的公式求出a,b,c的关系以及函数的解析式,求函数的极值,根据极值和零点的关系进行求解即可.
解答 解:∵f(x)=ax3+bx2+cx+1
∴f′(x)=3ax2+2bx+c
又∵f′(x)=3ax(x-1)=3ax2-3ax,
∴2b=-3a,c=0,即b=-$\frac{3}{2}$a,c=0,
则f(x)=ax3-$\frac{3}{2}$ax2+1,
∵a>2,
∴-$\frac{1}{2}$a+1<0,
∴f(1)=-$\frac{1}{2}$a+1<0,
又f(0)=1>0,
当x变化时,f′(x)与f(x)的变化如表所示:
| x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | ↓ | ↑ |
故选:D.
点评 本题主要考查求函数零点的个数,求函数的导数,利用函数极值和函数单调性之间的关系是解决本题的关键.属于中档题型.

练习册系列答案
相关题目
17.直线l 交椭圆$\frac{x^2}{8}+\frac{y^2}{4}$=1于M、N两点,椭圆的上顶点为B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是( )
| A. | 2x-3y-9=0 | B. | 3x-2y-11=0 | C. | 3x+2y-7=0 | D. | x-y-5=0 |
4.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线C2:x=$\frac{1}{8}$y2的焦点重合,直线l为bx-ay+8=0,P为C2上一个动点,P到直线l的距离为d1,到C2准线的距离为d2,当d1+d2的最小值为5时,C1的方程为( )
| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
1.在一次跳伞训练中,甲、乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员降落在指定范围”可表示为( )
| A. | (¬p)∨(¬p) | B. | ¬((¬p)∧(¬p)) | C. | (¬p)∧(¬p) | D. | ¬(p∨p) |
2.不等式|x+3|<4的解是( )
| A. | {x|x<-7} | B. | {x|-7<x<1} | C. | {x|x>1} | D. | {x|x<-7或x>1} |
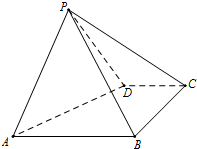 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.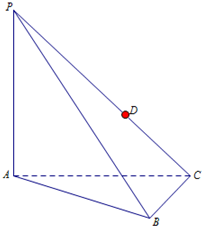 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.