题目内容
9.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为{an}的前n项和,则$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$的值为2.分析 由题意可得:a3=a1+2d,a4=a1+3d.结合a1、a3、a4成等比数列,得到a1=-4d,进而根据等差数列的通项公式化简所求的式子即可得出答案.
解答 解:设等差数列的公差为d,首项为a1,
所以a3=a1+2d,a4=a1+3d.
因为a1、a3、a4成等比数列,
所以(a1+2d)2=a1(a1+3d),解得:a1=-4d.
所以$\frac{{S}_{3}-{S}_{2}}{{S}_{5}-{S}_{3}}$=$\frac{{a}_{1}+2d}{2{a}_{1}+7d}$=2,
故答案为:2.
点评 解决此类问题的关键是熟练掌握等比数列与等差数列的性质,利用性质解决问题.

练习册系列答案
相关题目
2.不等式|x+3|<4的解是( )
| A. | {x|x<-7} | B. | {x|-7<x<1} | C. | {x|x>1} | D. | {x|x<-7或x>1} |
17.设i是虚数单位,则复数1-2i+3i2-4i3等于( )
| A. | -2-6i | B. | -2+2i | C. | 4+2i | D. | 4-6i |
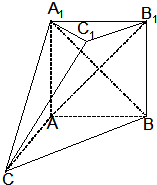 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1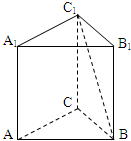 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
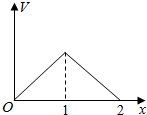
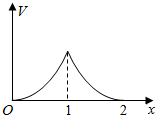
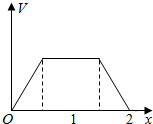
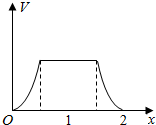
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.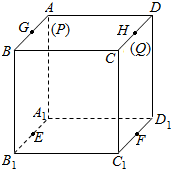 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )