题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≤0}\\{1-3x,x>0}\end{array}\right.$,若f(2a2-3)>f(5a),则实数a的取值范围是(-$\frac{1}{2}$,3).分析 结合指数函数和一次函数的单调性可判断函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≤0}\\{1-3x,x>0}\end{array}\right.$的R上为减函数,进而将不等式f(2a2-3)>f(5a)化为2a2-3<5a,解得答案.
解答 解:∵y=${(\frac{1}{2})}^{x}$与y=1-3x均为减函数,
且当x=0时,${(\frac{1}{2})}^{x}$=1-3x=1,
故函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≤0}\\{1-3x,x>0}\end{array}\right.$的R上为减函数,
若f(2a2-3)>f(5a),则2a2-3<5a,
解得:a∈(-$\frac{1}{2}$,3),
故实数a的取值范围是(-$\frac{1}{2}$,3),
故答案为:(-$\frac{1}{2}$,3)
点评 本题考查的知识点是函数的单调性,分段函数的应用,难度不大,属于基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
1.在一次跳伞训练中,甲、乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员降落在指定范围”可表示为( )
| A. | (¬p)∨(¬p) | B. | ¬((¬p)∧(¬p)) | C. | (¬p)∧(¬p) | D. | ¬(p∨p) |
2.不等式|x+3|<4的解是( )
| A. | {x|x<-7} | B. | {x|-7<x<1} | C. | {x|x>1} | D. | {x|x<-7或x>1} |
16.由观测的样本数据算得变量x与y满足线性回归方程$\widehaty=0.6x-0.5$,已知样本平均数$\overline x=5$,则样本平均数$\overline y$的值为( )
| A. | 0.5 | B. | 1.5 | C. | 2.5 | D. | 3.5 |
17.设i是虚数单位,则复数1-2i+3i2-4i3等于( )
| A. | -2-6i | B. | -2+2i | C. | 4+2i | D. | 4-6i |
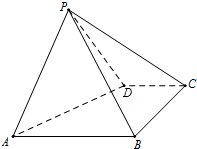 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.