题目内容
17.设O、A、B、C为平面上四个点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$且$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$,$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$=$\overrightarrow{c}$•$\overrightarrow{a}$=-1,则|$\overrightarrow{a}$|+|$\overrightarrow{b}$|+|$\overrightarrow{c}$|=$3\sqrt{2}$.分析 把$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$直接平方、移项后平方,再利用$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$=$\overrightarrow{c}$•$\overrightarrow{a}$=-1,可求得答案.
解答 解:∵$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$,$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$•$\overrightarrow{c}$=$\overrightarrow{c}$•$\overrightarrow{a}$=-1,
∴$|\overrightarrow{a}{|}^{2}+|\\;\overrightarrow{b}\\;{|}^{2}+|\\;\overrightarrow{c}{|}^{2}-6=0$$|\overrightarrow{b}{|}^{2}+|\overrightarrow{c}{|}^{2}-6=0$,①
把$\overrightarrow{a}$+$\overrightarrow{b}=-\overrightarrow{c}$两边平方得${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}={\overrightarrow{c}}^{2}$,②
由①知${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}=6-{\overrightarrow{c}}^{2}$,③
由②③知,$|\overrightarrow{c}{|}^{2}=2$,
$|\overrightarrow{c}|=\sqrt{2}$,
把$\overrightarrow{a}+\overrightarrow{c}=-\overrightarrow{b}$两边平方得${\overrightarrow{a}}^{2}+{\overrightarrow{c}}^{2}-2={\overrightarrow{b}}^{2}$,
$|\overrightarrow{a}{|}^{2}=|\overrightarrow{b}{|}^{2}=2$,
∴$|\overrightarrow{a}|=|\overrightarrow{b}|=\sqrt{2}$,
则|$\overrightarrow{a}$|+|$\overrightarrow{b}$|+|$\overrightarrow{c}$|=$3\sqrt{2}$,
故答案为$3\sqrt{2}\\;\\;\$.
点评 本题考查向量的数量积的运算,向量的模的求法,关键是将条件进行转化变形.

 口算能手系列答案
口算能手系列答案
| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
| A. | {x|x<-7} | B. | {x|-7<x<1} | C. | {x|x>1} | D. | {x|x<-7或x>1} |
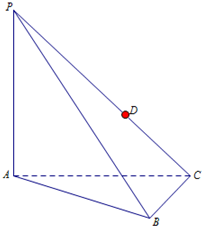 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.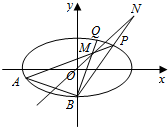 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.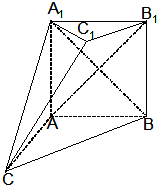 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1