题目内容
11.数列{an}中,若Sn=n2an,a1=$\frac{1}{2}$,则an=$\frac{1}{n(n+1)}$.分析 利用an+1=Sn+1-Sn,整理出an的递推式,进而用叠乘法求得an.
解答 解:∵Sn=n2an,∴Sn+1=(n+1)2an+1,
两式相减得:an+1=Sn+1-Sn=(n+1)2an+1-n2an,
∴n2an=n(n+2)an+1,即nan=(n+2)an+1,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{(n+1)-1}{(n+1)+1}$,即$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{n-1}{n+1}$,
∴$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{3}}{{a}_{2}}$•$\frac{{a}_{2}}{{a}_{1}}$=$\frac{n-1}{n+1}$•$\frac{n-2}{n}$•…•$\frac{1}{3}$•$\frac{1}{2}$,
∴an=$\frac{n-1}{n+1}$•$\frac{n-2}{n}$•…•$\frac{2}{4}$•$\frac{1}{3}$•$\frac{1}{2}$=$\frac{1}{n(n+1)}$,
故答案为:$\frac{1}{n(n+1)}$.
点评 本题主要考查了数列的递推式.数列的递推式是高考中常考的题型,涉及数列的通项公式,求和问题,数列与不等式的综合等问题,注意解题方法的积累,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
4.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线C2:x=$\frac{1}{8}$y2的焦点重合,直线l为bx-ay+8=0,P为C2上一个动点,P到直线l的距离为d1,到C2准线的距离为d2,当d1+d2的最小值为5时,C1的方程为( )
| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
2.不等式|x+3|<4的解是( )
| A. | {x|x<-7} | B. | {x|-7<x<1} | C. | {x|x>1} | D. | {x|x<-7或x>1} |
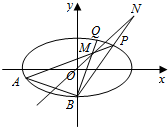 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.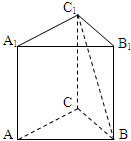 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.